集成学习方法小结

Bootstrap、Bagging以及Boosting都是机器学习中一些常见的概念，而且很相似同时又有一些关联。

Bootstrap

Bootstrap是统计学习中一种抽样方法

机器学习本质是利用有限的训练数据集（样本）来学习客观的数据分布规律（总体），因此是一种利用样本评估总体的方法。在此基础上，Bootstrap进一步用样本的样本来评估，也就是从训练数据集中再次采样。Bootstrap的采样是有放回的重采样，对于小样本的表现效果很好，通过方差的估计来构造置信度区间等等，可使得其运用范围。特别是当我们不知道训练样本的数据分布的时候，Bootstrap 非常有用。

Bootstrap的工作原理可以用网上的一个例子来说明：

问题：我要统计鱼塘里面的鱼的条数，怎么统计呢？假设鱼塘总共有鱼1000条。

步骤：

1. 承包鱼塘，不让别人捞鱼(规定总体分布不变)。
2. 自己捞鱼，捞100条，都打上标签(构造样本)
3. 把鱼放回鱼塘，休息一晚(使之混入整个鱼群，确保之后抽样随机)
4. 开始捞鱼，每次捞100条，数一下，自己昨天标记的鱼有多少条，占比多少(一次重采样取分布)，然后将鱼放回去（有放回）。
5. 重复3，4步骤n次。建立分布。

假设一下，第一次重新捕鱼100条，发现里面有标记的鱼12条，记下为12%，放回去，再捕鱼100条，发现标记的为9条，记下9%，重复重复好多次之后，假设取置信区间95%，你会发现，每次捕鱼平均在10条左右有标记，所以，我们可以大致推测出鱼塘有1000条左右。其实是一个很简单的类似于一个比例问题。

为什么只在小样本的时候Bootstrap效果较好？你这样想，如果我想统计大海里有多少鱼，你标记100000条也没用啊，因为实际数量太过庞大，你取的样本相比于太过渺小，最实际的就是，你下次再捕100000的时候，发现一条都没有标记…

Bootstrap方法最初由美国斯坦福大学统计学教授Efron在1977年提出。作为一种崭新的增广样本统计方法，Bootstrap方法为解决小规模子样试验评估问题提供了很好的思路。当初，Efron教授将他的论文投给了统计学领域的一流刊物《The Annals of Statistics》，但在被该刊接受之前，这篇后来被奉为扛鼎之作的文章曾经被杂志编辑毫不客气地拒绝过，理由是“太简单”。从某种角度来讲，这也是有道理的，Bootstrap的思想的确再简单不过，但后来大量的事实证明，这样一种简单的思想却给很多统计学理论带来了深远的影响，并为一些传统难题提供了有效的解决办法。Bootstrap方法提出之后的10年间，统计学家对它在各个领域的扩展和应用做了大量研究，到了20世纪90年代，这些成果被陆续呈现出来，而且论述更加全面、系统。

Bagging

Bagging是一种集成学习方法，其思想是通过样本的重采样构造不同的数据集来训练不同的基模型而其采样的方法就是使用Bootstrap，而且一般Bagging方法中采样的数量和原样本的数量，具体采样步骤如下：

1. 从所有样本中随机抽取一个样本
2. 将1中样本放回到样本集中，充分混合。
3. 重复步骤1和2，直到满足采样数目要求。

正式因为这种采样的方式，因此Bagging又被称为Bootstrap aggregation。对于一个样本，它在一个包含 $n$ 个样本的训练集中随机采样，则每次被采到的概率是 $1/n$ ，则不被抽取的概率是 $1-1/n$ 。若抽取次数和数据集相同，则抽取完毕，一个样本不被抽取的概率是 $(1-\frac{1}{n})^n$ ，当 $m \to \infty$ ， $(1-\frac{1}{m})^m \to \frac{1}{e} \simeq 0.368$ 。也就是说在bagging的每轮随机抽取中，训练集中大约有36.8%的数据没有被采样集采集中。对于这部分大约36.8%的没有被采样到的数据，我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合，因此可以用来检测模型的泛化能力。

Bagging方法的示意图如下：

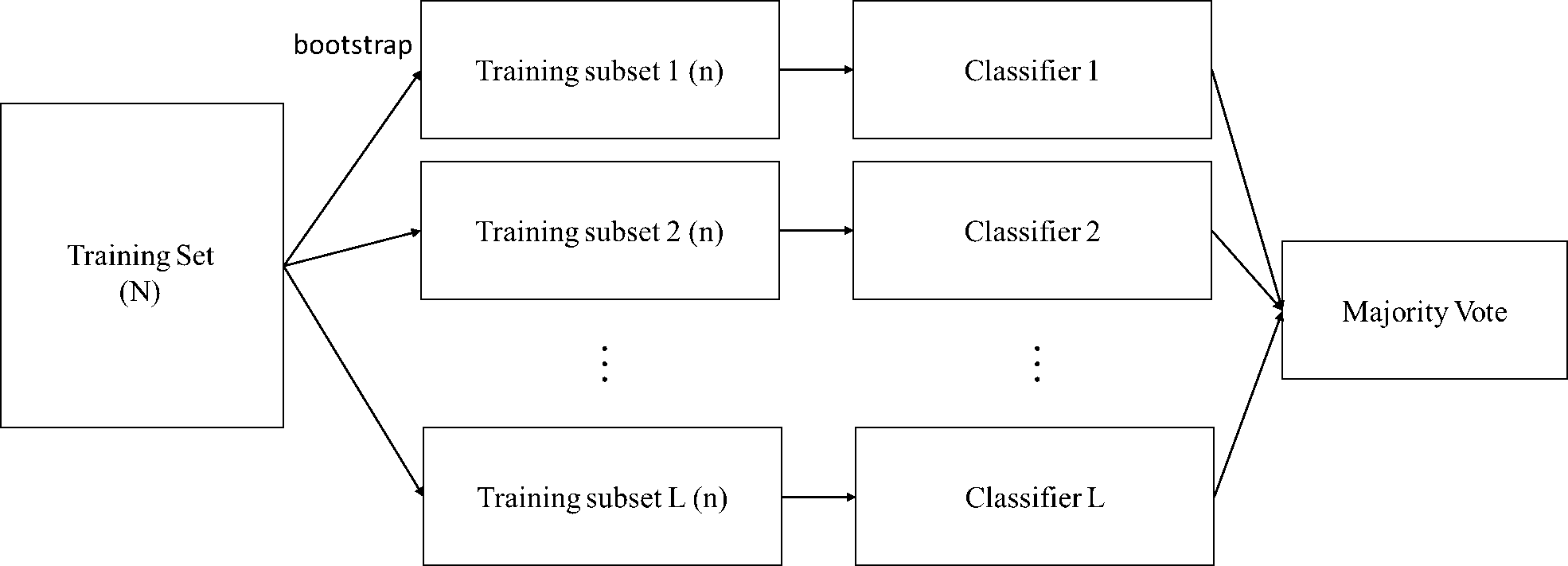
1. 从样本集中用Bootstrap采样选出n个训练样本(放回，因为别的分类器抽训练样本的时候也要用)
2. 在所有属性上，用这n个样本训练分类器（CART or SVM or …）
3. 重复以上两步m次，就可以得到m个分类器（CART or SVM or …）
4. 将数据放在这m个分类器上跑，最后投票机制(多数服从少数)看到底分到哪一类(分类问题)

Bagging方法的代表性算法就是随机森林(Random Forest, RF)。

随机森林

首先，RF使用了CART决策树作为弱学习器；第二，在使用决策树的基础上，RF对决策树的建立做了改进，对于普通的决策树，我们会在节点上所有的 $n$ 个样本特征中选择一个最优的特征来做决策树的左右子树划分，但是RF通过随机选择节点上的一部分样本特征，这个数字小于 $n$ ，假设为 $n{sub}$ ，然后在这些随机选择的 $n{sub}$ 个样本特征中，选择一个最优的特征来做决策树的左右子树划分。这样进一步增强了模型的泛化能力。

如果 $n{sub}=n$ ，则此时RF的决策树和普通的CART决策树没有区别， $n{sub}$ 越小，则模型越健壮，当然也就越难拟合。也就是说模型的方差会减小，但是偏差变大。在实际案例中，一般会通过交叉验证调参获取一个合适的 $n_{sub}$ 。

简单总结一下RF的算法：

输入：样本集 $D={(x_,y_1), (x_2,y_2), …(x_m,y_m)}$ ，弱分类器迭代次数 $T$ 。
输出：最终的强分类器 $f(x)$ 。

1. 对于训练阶段 $t=1, 2, …T$ :
   (1) 对训练集进行 $m$ 次有放回的随机重采样，得到包含 $m$ 个训练样本的 $D{t}$ ；
   (2）构建第 $t$ 个决策树模型 $G{t}(x)$ ，在训练决策树模型的节点的时候，在节点上所有的样本特征中随机选择一部分样本特征；
   (3) 在这些随机选择的部分样本特征中随机选择一个最优的特征来做决策树的左右子树划分；
   (4) 重复步骤3，直到构建完成决策树。
2. 如果是分类算法预测，则 $T$ 个弱学习器投票最多的类别作为最终结果；若是回归算法，则使用T个弱学习器的算术平均作为最终模型的输出结果。

RF的主要优点有：

• 各个弱分类器之间没有关联，训练可以高度并行化，对于大数据时代的大样本训练速度有优势。
• 由于可以随机选择决策树节点划分特征，这样在样本特征维度很高的时候，仍然能高效的训练模型。
• 在训练后，可以给出各个特征对于输出的重要性。
• 由于采用了随机采样，训练出的模型的方差小，泛化能力强。
• 相对于Boosting系列的Adaboost和GBDT， RF实现比较简单。
• 对部分特征缺失不敏感。

RF的主要缺点有：

• 在某些噪音比较大的样本集上，RF模型容易陷入过拟合。
• 取值划分比较多的特征容易对RF的决策产生更大的影响，从而影响拟合的模型的效果。

Boosting

Boosting是一种框架算法，用来提高弱分类器准确度的方法，这种方法通过构造一个预测函数序列，然后以一定的方式将他们组合成为一个准确度较高的预测函数。Boosting算法更加关注错分的样本，这点和Active Learning的寻找最有价值的训练样本有点遥相呼应的感觉。

通俗一点来说：Boosting是一种迭代算法，针对同一个训练集训练不同的分类器(弱分类器)，然后进行分类，对于分类正确的样本权值低，分类错误的样本权值高（通常是边界附近的样本），最后的强分类器是很多弱分类器的线性叠加（加权组合，权重和分类器精度有关）。实际上就是一个简单的弱分类算法提升(boost)的过程。

Boosting与Baggin方法不同之处在于不同的分类器之间是有关联的，Boosting方法示意图如下：

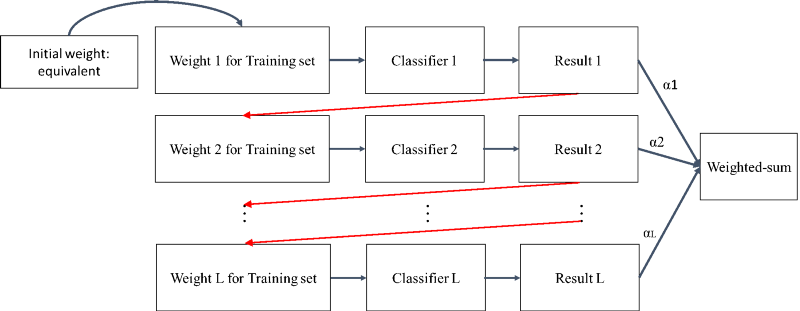
从图中可以看出，Boosting算法的工作机制是首先从训练集用初始权重训练出一个弱分类器Classifier1，根据弱学习的学习结果Result1表现来更新训练样本的权重，使得之前Classifier1学习误差率高的训练样本点的权重变高，使得这些误差率高的点在后面的Classifier2中得到更多的重视。然后基于调整权重后的训练集来训练Classifier2，如此重复进行，直到弱学习器数达到事先指定的数目L，最终将这L个弱学习器通过集合策略进行整合，得到最终的强学习器。　　

Boosting算法中存在几个如下的细节还需要弄明白：

1. 如何计算学习误差率 $e$ ？
2. 如何得到弱分类器的权重系数 $\alpha$ ？
3. 如何更新样本的权重？
4. 如何将各个弱分类器结合起来？

这4个问题对于Boosting家族算法都是需要解决的问题，下面结合AdaBoost算法来探究一下。

AdaBoost

对于AdaBoost学习器，可以解决分类问题和回归问题，不同问题，上述4个方面的细节实现也不一样。

分类问题

对于分类问题，假设我们的训练集样本是：

$$T=\{(x_,y_1),(x_2,y_2), ...(x_m,y_m)\}$$

训练集在第 $k$ 个弱分类器的输出权重为：

$$D(k) = (w_{k1}, w_{k2}, ...w_{km}) ;\;\; w_{1i}=\frac{1}{m};\;\; i =1,2...m$$

下面针对上述4个方面分别进行讨论：

误差率

首先来看看分类问题的误差率。由于多元分类是二元分类的推广，这里假设我们是二元分类问题，输出为 ${-1, 1}$ ，则第 $k$ 个弱分类器 $G_{k}(x)$ 在训练集上的加权误差率为：

$$e_k = P(G_k(x_i) \neq y_i) = \sum\limits_{i=1}^{m}w_{ki}I(G_k(x_i) \neq y_i)$$

其中 $I(G_k(x_i) \neq y_i)$ 表示预测结果和标签的对比结果。

分类器权重系数更新

接下来看看弱分类器的权重系数。对于二分类问题，第 $k$ 个弱分类器 $G_{k}(x)$ 的权重系数为：

$$\alpha_k = \frac{1}{2}log\frac{1-e_k}{e_k}$$

从式子可以看出，如果分类误差率 $e_k$ 越大，则其权重系数 $\alpha_k$ 越小。

样本权重更新

$$w_{k+1,i} = \frac{w_{ki}}{Z_K}exp(-\alpha_ky_iG_k(x_i))$$

这里 $Z_k$ 是规范化因子：

$$Z_k = \sum\limits_{i=1}^{m}w_{ki}exp(-\alpha_ky_iG_k(x_i))$$

从 $w_{k+1,i}$ 计算公式可以看出，如果第 $i$ 个样本分类错误，则 $y_iG_k(x_i) < 0$ ，导致样本的权重在第 $k+1$ 个弱分类器中增大，反之亦然。

分类器结合策略

AdaBoost采用的是加权表决法，最终的强分类器为：

$$f(x) = sign(\sum\limits_{k=1}^{K}\alpha_kG_k(x))$$

回归问题

由于Adaboost的回归问题有很多变种，这里我们以Adaboost R2算法为准。

误差率

首先计算训练上的最大误差

$$E_k = max|y_i - G_k(x_i)|\; i=1,2...m$$

然后计算每个样本的相对误差：

$$e_{ki}= \frac{|y_i - G_k(x_i)|}{E_k}$$

这里是误差损失为线性时的情况，也可以用平方误差：

$$e_{ki}= \frac{(y_i - G_k(x_i))^2}{E_k^2}$$

或者指数误差：

$$e_{ki}= 1 - exp(\frac{-y_i + G_k(x_i))}{E_k})$$

最终得到第 $k$ 个弱学习器的误差率：

$$e_k = \sum\limits_{i=1}^{m}w_{ki}e_{ki}$$

弱学习器权重系数更新

$$\alpha_k =\frac{e_k}{1-e_k}$$

样本权重更新

$$w_{k+1,i} = \frac{w_{ki}}{Z_k}\alpha_k^{1-e_{ki}}$$

这里 $Z_k$ 是规范化因子：

$$Z_k = \sum\limits_{i=1}^{m}w_{ki}\alpha_k^{1-e_{ki}}$$

结合策略

和分类问题稍有不同，采用的是对加权的弱学习器取权重中位数对应的弱学习器作为强学习器的方法，最终的强回归器为：

$$f(x) = G_{k^*}(x)$$

其中， $G_{k^*}(x)$ 是所有 $ln\frac{1}{\alpha_k}, k=1,2,….K$ 的中位数值对应序号 $k^*$ 对应的弱学习器。

AdaBoost损失函数

AdaBoost上述的学习器的权重系数以及样本权重的更新公式并不是凭空出现的，都是从Adaboost的损失函数推导出来。

具体可见AdaBoost损失函数优化，本文就不具体展开了。

AdaBoost算法流程

上面4个问题解决了，AdaBoost的流程也就弄明白了：

1. 初始化样本权重
2. 使用有权重的样本集训练弱学习器（包括分类和回归）
3. 计算弱学习器的误差
4. 更新弱学习器的系数
5. 更新样本权重分布
6. 重复2~5来构建多个弱学习器
7. 根据结合策略，利用多个弱学习器构建最终的强学习器。

Bagging，Boosting二者之间的区别

Bagging和Boosting的区别：

样本选择上：

• Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。
• Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

样例权重：

• Bagging：使用均匀取样，每个样例的权重相等
• Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

预测函数：

• Bagging：所有预测函数的权重相等。
• Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

并行计算：

• Bagging：各个预测函数可以并行生成
• Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

参考资料

• https://www.jianshu.com/p/708dff71df3a
• http://www.cnblogs.com/pinard/p/6156009.html