主成分分析(PCA)在机器学习领域主要的作用就是降维,其背后有严格的数学理论支持。
基于协方差和特征向量的推导
考虑一组 $M$ 个观测数据 $\boldsymbol X$,每个数据具有 $n$ 维的特征。降维的目的就是降低特征的数目,也就是将原始特征映射到 $d < n$ 维的特征空间中。同时最大化投影数据的方差,也就是维持投影后的特征的可分性。
了解了基本含义再来看个例子,先看一个直观的图像, 下图为400个二维的数据样本,这二维的数据相关性很大。直观的感觉就是当数据投影到绿色的箭头的方向上时,方差最大。
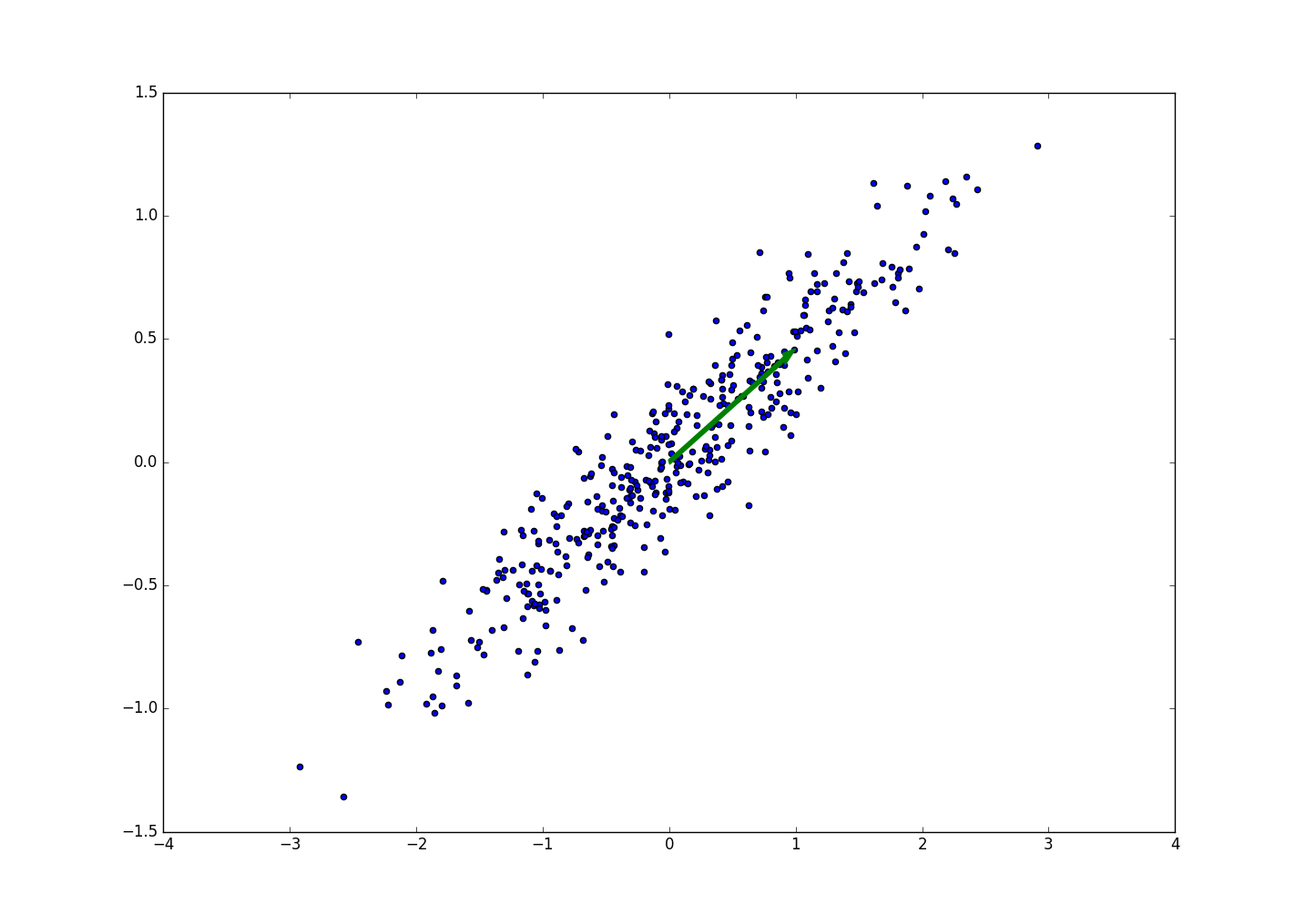
换句话说,当所有点映射到一条直线时(二维变一维),这个直线的方向为绿色箭头方向的时候,可分性最好,也就是最大程度上维持了特征。我们也可以认为绿色箭头代表的一维空间是这批数据的主成分,而绿色箭头的正交方向就是我们丢弃的维度。(绿色箭头和其正交方向组成的二维空间就是图中坐标系代表的二维空间,只不过旋转了一个角度)
现在考虑将数据投射到低维的情况,也就是在 $n$ 维的向量空间找到一个向量 $\boldsymbol u$,当数据集中的数据投射到该向量上时投射后的数据集具有最大方差,实际上只需要找出向量 $\boldsymbol u$ 的方向即可。所以可以约束向量 $\boldsymbol u$ 的模为1,对于二维投影,向量的投影即是内积,于是数据投射到该向量上的大小就是样本的特征向量 $\boldsymbol x_m$ 点乘向量 $\boldsymbol u$ 。假设映射后的向量维度是 $d$,则 $\boldsymbol u$ 的大小是 $d \cdot n$,映射操作是 $\boldsymbol u\boldsymbol x_m$。
投射后的方差为:
因此问题的目标就转换为在约束向量 $\boldsymbol u$ 为单位向量的情况下,最大化 $\boldsymbol u^T \boldsymbol S \boldsymbol u$。其中 $\boldsymbol x^-$ 为观测样本集在各个维度上的均值, $\boldsymbol S$ 为观测样本集的协方差矩阵:
$\boldsymbol S=\frac{1}{M}\sum_{}{}(\boldsymbol x_m- \boldsymbol x^-)(\boldsymbol x_m - \boldsymbol x^-)^T$
采用拉格朗日乘子法将约束优化问题转为无约束优化得到下式:
$\boldsymbol u^T \boldsymbol S \boldsymbol u + \lambda (1 - \boldsymbol u^T \boldsymbol u)$
对上式中 $\boldsymbol u$ 求偏导,然后设为0,得到:
$\boldsymbol S \boldsymbol u = \lambda \boldsymbol u$
上式中 $\boldsymbol S$ 是一个 $n \cdot n$ 的矩阵, $\lambda$ 是一个标量, $\boldsymbol u$ 为 $n$ 维向量。很明显, $\boldsymbol u$ 为矩阵 $\boldsymbol S$ 的特征向量,表示映射后的低维特征方向, $\lambda$ 是对应的特征值。
以上就是从映射求解后方差最大这个思路来理解和推导的PCA的数学原理。
对角化协方差矩阵
PCA另一个数学理解角度就是对角化协方差矩阵。我们知道协方差矩阵表示不同特征维度之间的相关性。我们的优化目标:首先利用线性变换,将原始数据变换为一组各维度线性无关的表示,然后在线性无关的各维度中,挑选主要的特征分量,忽略次要的,这就是降维。就是找到低维特征空间中的一组正交基来表示高纬度的特征信息,说白了就是要求映射得到的低维特征之间的线性相关性为0,且各个维度特征之间的方差最大。
由于协方差矩阵的特殊性,协方差矩阵是可以对角化的,也就是存在一个矩阵 $P$,满足 $PSP^T$ 是一个对角矩阵,对角元素就是各个特征维度的权重系数,非对角元素为0,也就是不同维度之间的线性相关性为0。只需要找到这个变换矩阵 $P$,然后利用选择前 $k$ 行来乘以 $X$,就得到了 $X$ 降维后的特征。具体推导可以参见:PCA的数学原理
PCA降维的步骤总结:
设有 $m$ 条数据,每个数据有 $n$ 维特征,原始数据组成 $n$ 行,$m$ 列的矩阵 $X$
- 将 $X$ 的每一行(表示一个维度的特征)进行零均值化,即减去这一行的均值;
- 求原始数据的协方差矩阵:$C=\frac{1}{m}XX^T$;
- 求协方差矩阵的特征值以及对应的特征向量;
- 将特征向量对应特征值大小从上到下,按行排列,取前 $k$ 行组成变换矩阵 $P$ (大小是 $k \cdot n$ );
- $Y=PX$ 即为降维后的矩阵,$Y$ 的大小是 $k \cdot m$。