目前所采用的扩散模型大都是来自于 2020 年的工作 DDPM。DDPM 对之前的扩散模型进行了简化,并通过变分推断(variational inference)来进行建模,这主要是因为扩散模型也是一个隐变量模型(latent variable model),相比 VAE 这样的隐变量模型,扩散模型的隐变量是和原始数据是同维度的,而且推理过程(即扩散过程)往往是固定的。
引言
扩散模型包括两个过程:前向过程(forward process)和反向过程(reverse process),其中前向过程又称为扩散过程(diffusion process),如下图所示。无论是前向过程还是反向过程都是一个参数化的马尔可夫链(Markov chain),其中反向过程可以用来生成数据,这里我们将通过变分推断来进行建模和求解。
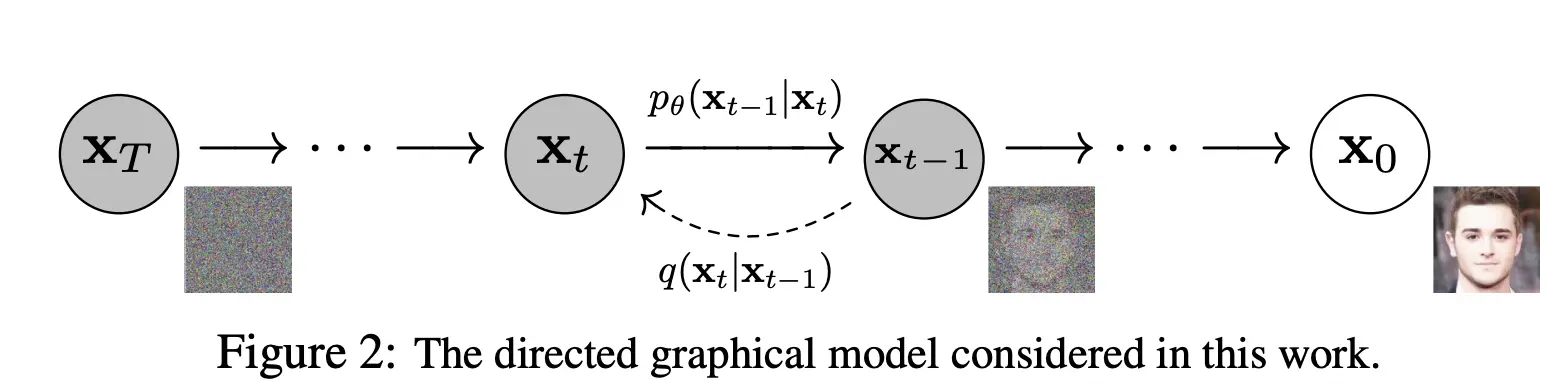
前向扩散过程(Forward Diffusion Process)
解释扩散之前先介绍一个基本的数学表示:
一个正态分布,其中 $\mu$ 是均值,$\Sigma$ 是协方差矩阵。在这个过程中,$x_t$ 服从一个 $\mu$ 为均值、$\Sigma$ 为协方差矩阵的正态分布。
扩散就是对图像数据进行加噪声的过程,最核心的数学公式表示如下:
$x_0$ 是原始数据,$x_t$ 是在 $t$ 时刻的样本,$\mathcal{N}$ 表示正态分布,$\beta_t$ 表示在第 $t$ 步的方差(噪音量),它是一个介于 0 和 1 之间的值,$\sqrt{1 - \beta_t}$ 表示输入数据的缩放系数,$\beta_t \mathbf{I}$ 表示加的噪音的方差。
这个公式表示,给定 $x{t-1}$ 的情况下,$x_t$ 是以 $\sqrt{1 - \beta_t} x{t-1}$ 为均值、$\betat \mathbf{I}$ 为协方差矩阵的正态分布。可以简单理解为,$x_t$ 是 $x{t-1}$ 加上高斯噪音后的结果。
前向过程就是这么简单。当我们逐渐加大 $\beta_t$ 时,$x_t$ 逐渐变得模糊,最终变成一个高斯噪声图像。
这里也有一个推导,就是通过 $x_0$,可以直接表示 $x_T$,因为高斯分布可以直接相加。
逆向生成过程(Reverse Generation Process)
训练过程中,DDPM 学习从噪声生成数据的逆向过程。我们假设逆向过程也是一个高斯过程,但参数未知:
这里,模型的任务是学习 $\mu\theta$ 和 $\sigma\theta$ 的参数化形式,使得可以从噪声生成逼真的数据样本。
训练目标
训练的目标是最小化前向过程和逆向过程之间的差异。具体来说,训练目标可以表示为以下 KL 散度的和:
每一个 KL 项衡量在第 $t$ 个时间步长上真实分布和模型估计分布之间的差异。
损失函数
为了简化训练过程,我们可以重参数化损失函数为一个去噪过程的预测任务。目标变为预测加入噪声的程度(噪声项)的均值和方差。
这里重参数的推导很长,可以网上找一下。
其中 $\epsilon$ 是在前向过程加入的数据噪声,$\epsilon_\theta$ 是通过神经网络预测的噪声。所以神经网络的任务就是抽取一个 $t$(1~$T$ 之间),通过 $x_0$ 和加噪过程,计算得到 $x_t$,然后神经网络预测噪声,计算预测的噪声和实际噪声的分布差异。
训练步骤
- 采样数据 $x_0$ 从真实数据分布中。
- 采样噪声 $\epsilon$ 从标准正态分布中。
- 计算 $x_t$ 通过前向扩散过程,将噪声加入数据。
- 计算预测的噪声 $\epsilon_\theta(x_t, t)$ 使用神经网络。
- 计算损失 $L$ 并通过反向传播更新模型参数。
生成步骤
生成数据时,从标准正态分布中采样 $x_T$,然后逐步通过逆向生成过程去噪,生成数据 $x_0$。
在 DDPM 中,会将原始图像的像素值从 [0, 255] 范围归一化到 [-1, 1],像素值属于离散化值。
背后原理
DDPM 通过一个称为”马尔科夫链”的过程,逐步将噪声转化为数据。其核心思想是分阶段进行去噪,每个阶段只去除一小部分噪声,使得每一步的去噪过程更为简单和稳定。
总的来说,DDPM 在生成任务中表现出色,特别是生成图像和其他复杂结构的数据类型。这是因为它通过多步生成过程有效地捕捉了数据的复杂结构和细节。
DDPM 的推导过程中,最重要的就是重参数技巧,这个技巧在很多生成模型中都有应用,比如 VAE、GAN 等。