ResNet 算是深度学习里程碑之作了,我平时接触也比较多,写一篇文章做一些记录总结。
引言:为什么会有 ResNet?
神经网络叠的越深,则学习出的效果就一定会越好吗?
答案无疑是否定的,人们发现当模型层数增加到某种程度,模型的效果将会不升反降。也就是说,深度模型发生了退化(degradation)情况。
那么,为什么会出现这种情况?我们从以下几点来分析。
过拟合(overfitting)问题
首先看一下吴恩达机器学习公开课中所描述的过拟合问题:
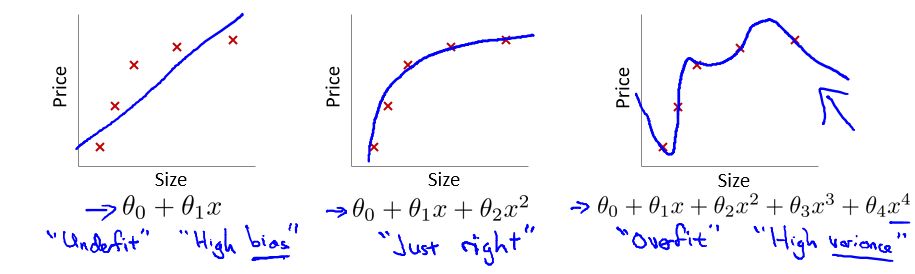
在这个多项式回归问题中,左边的模型是欠拟合(underfit)的此时有很高的偏差(high bias),中间的拟合比较成功,而右边则是典型的过拟合(overfit),此时由于模型过于复杂,导致了高方差(high variance)。
然而,很明显当前CNN面临的效果退化不是因为过拟合,因为过拟合的现象是”高方差,低偏差”,即测试误差大而训练误差小。但实际上,深层CNN的训练误差和测试误差都很大。所以也不完全是过拟合的问题。
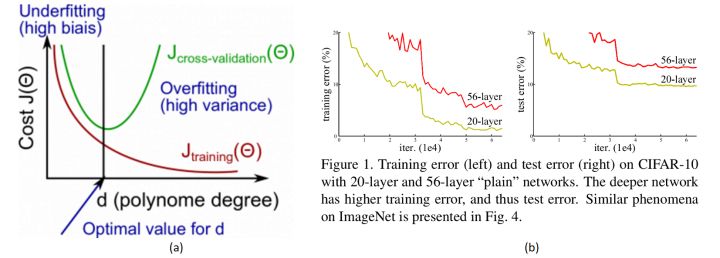
梯度消失和爆炸(Gradient vanishing/exploding)
除此之外,最受人认可的原因就是“梯度爆炸/消失(弥散)”了。为了理解什么是梯度弥散,首先回顾一下反向传播的知识。
假设我们现在需要计算一个函数:$f(x,y,z)=(x+y) \times z$ 在 $x=-2,y=5,z=-4$ 时的梯度,那么计算流程如下:
- 前向传播计算 $f(x=-2,y=5,z=-4)$ 的结果为 -12。
- 令 $q=x+y$ ,可以推导反向传播:
上面的前向传播和反向传播学过微积分的都应该明白。反向传播其实就是输出端梯度通过链式法则向输入端传播的过程,这里假设输出端初始的梯度为 1,也就是输出端对自身求导等于 1。
观察上述反向传播,不难发现,在输出端梯度的模值,经过回传扩大了3~4倍。
这是由于反向传播结果的数值大小不止取决于求导的式子,很大程度上也取决于输入的模值。当计算图每次输入的模值都大于1,那么经过很多层回传,梯度将不可避免地呈几何倍数增长(每次都变成 3~4 倍,重复上万次,想象一下 3 的 10000 次方有多大……),直到Nan。这就是梯度爆炸现象。
当然反过来,如果我们每个阶段输入的模恒小于 1,那么梯度也将不可避免地呈几何倍数下降(比如每次都变成原来的三分之一,重复一万次就是 3 的 -10000 次方),直到 0。这就是梯度消失现象。值得一提的是,由于人为的参数设置,梯度更倾向于消失而不是爆炸。
由于至今神经网络都以反向传播为参数更新的基础,所以梯度消失问题听起来很有道理。然而,事实也并非如此,至少不止如此。
我们现在无论用 Pytorch 还是 Tensorflow,都会自然而然地加上 Bacth Normalization,而 BN 的作用本质上也是控制每层输入的模值,因此梯度的爆炸/消失现象理应在很早就被解决了(至少解决了大半)。
不是过拟合,也不是梯度消失,这就很尴尬了……CNN 没有遇到我们熟知的两个老大难问题,却还是随着模型的加深而导致效果退化。无需任何数学论证,我们都会觉得这不符合常理。
为什么模型退化不符合常理?
He 在论文中举了一个例子,假设一个比较浅的网络已经可以达到不错的效果,那么即使之后堆上去的网络什么也不做,模型的效果也不会变差。而之前的深度网络出现退化问题,所以很明显什么都不做恰好是当前神经网络最难做到的东西之一。
MobileNet V2 的论文也提到过类似的现象,由于非线性激活函数 ReLU 的存在,每次输入到输出的过程都几乎是不可逆的(信息损失)。我们很难从输出反推回完整的输入。因此 MobileNet V2 论文中选择去掉低维的 ReLU 以保留特征信息。
我们可以认为,为了实现非线性,激活函数让特征在传播过程中丢失了信息,因此这类的神经网络都无法做到“恒等映射”。
因此,可以认为 Residual Learning 的初衷,其实是让模型的内部结构至少有恒等映射的能力。以保证在堆叠网络的过程中,网络至少不会因为继续堆叠而产生退化!
深度残差学习(Deep Residual Learning)
残差学习
前面分析得出,如果深层网络后面的层都是是恒等映射,那么模型就可以转化为一个浅层网络。那现在的问题就是如何得到恒等映射了。但是要让一个神经网络你和 $H(x)=x$ 其实是非常困难的。于是 He 等人换了一个思路,把网络设计为 $H(x) = F(x) + x$,即直接把恒等映射作为网络的一部分。就可以把问题转化为学习一个残差函数 $F(x) = H(x) - x$。
只要 $F(x)=0$,就构成了一个恒等映射 $H(x) = x$。 而且,拟合残差至少比拟合恒等映射容易得多。于是,就有了 Residual block 结构。
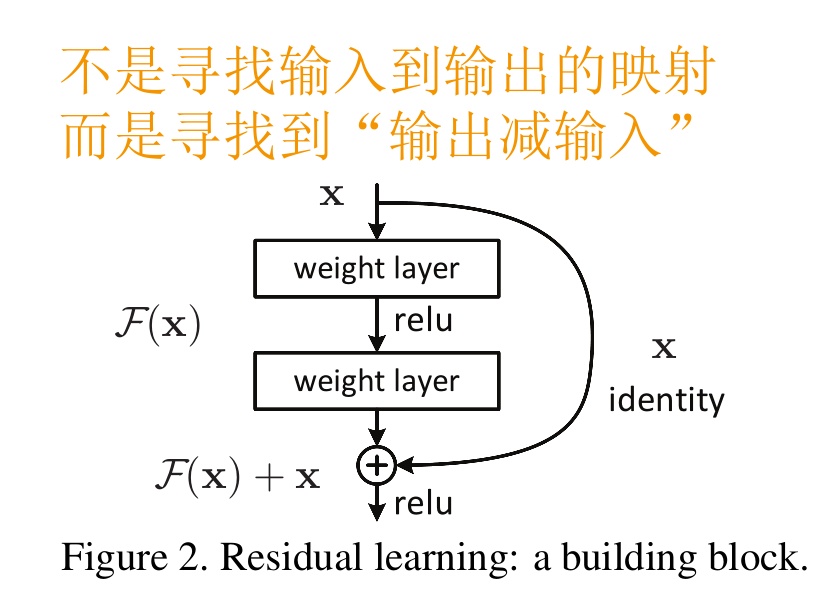
图中右侧的曲线叫做跳接(shortcut connection),通过跳接在激活函数前,将上一层(或几层)之前的输出与本层计算的输出相加,将求和的结果输入到激活函数中做为本层的输出。
用数学语言描述,假设 Residual Block 的输入为 $x$,则输出 $y$ 等于:$y=F(x, {W_i}) + x$。$F$ 就是我们要学习的目标,即输出和输入的残差 $y-x$ 。
上图中的计算可以表示为:$F=W_2/ \sigma(W_1x)$。也就是经过两个权重层和一个激活层。这里需要注意,一个 Residual Block 必须至少含有两个权重层,否则没有意义:$y=(W_1x) + x = (W_1 + 1) + x$。相当于权重加 1,加了和没加一样。
残差网络结构根据是否改变 feature map 大小又分为两种,也就是是否 down sample(空间减半,深度翻倍)。实际实现中就是在跳接过程中是否使用卷积进行维度和空间大小的改变。
What the question?
残差学习解决了模型退化的问题,但是模型退化是一个现象问题,其本质原因或者说深度 CNN 的本质问题是什么呢?
The Shattered Gradients Problem: If resnets are the answer, then what is the question?
论文大意是神经网络越来越深的时候,反传回来的梯度之间的相关性会越来越差,最后接近白噪声。因为我们知道图像是具备局部相关性的,那其实可以认为梯度也应该具备类似的相关性,这样更新的梯度才有意义,如果梯度接近白噪声,那梯度更新可能根本就是在做随机扰动。
论文认为即使 BN 过后梯度的模稳定在了正常范围内,但梯度的相关性实际上是随着层数增加持续衰减的。而经过证明,ResNet 可以有效减少这种相关性的衰减。大概从 $\frac {1} {2^L}$ 减小到 $\frac {1} {\sqrt(L)}$ 。这也验证了 ResNet 论文本身的观点,网络训练难度随着层数增长的速度不是线性,而至少是多项式等级的增长(如果该论文属实,则可能是指数级增长的)。
后续
在残差网络之后,跳接给网络的设计带来了很多新的思考。以 FPN(Feature Pyramid Network)为代表的跳接网络从语义的角度解决了深度网络的特征提取问题,那就是跳连接相加可以实现不同分辨率特征的组合,因为浅层容易有高分辨率但是低级语义的特征,而深层的特征有高级语义,但分辨率就很低了。
引入跳接实际上让模型自身有了更加“灵活”的结构,即在训练过程本身,模型可以选择在每一个部分是“更多进行卷积与非线性变换”还是“更多倾向于什么都不做”,抑或是将两者结合。模型在训练便可以自适应本身的结构。