最大似然估计和最大后验概率估计是概率论中应用很广泛的两个理论,之前的理解似是而非,因此查阅了一些资料,总结记录。
最大似然估计
最大似然估计(Maximum likelihood estimation, 简称 MLE)是概率论中最常见的应用理论之一,另一个是贝叶斯定理。最大似然估计通俗理解就是利用已知的样本结果信息,反推最有可能导致这个结果出现的模型参数。
换个角度想一想,在机器学习和深度学习任务中,我们学习的是什么?当一个模型确定的时候,我们学习的就是模型的参数啊。换句话说,极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。
似然(likelihood)这个词其实和概率(probability)是差不多的意思,Colins字典这么解释:The likelihood of something happening is how likely it is to happen. 你把 likelihood 换成 probability,这解释也读得通。但是在统计里面,似然函数和概率函数却是两个不同的概念(其实也很相近就是了)。
对于函数 $P(x|\theta)$,输入有两个:$x$ 表示某一个具体的数据,$\theta$ 表示模型的参数。
- 如果 $\theta$ 是已知确定的,$x$ 是变量,这个函数就称为概率函数(probability function),它描述对于不同的样本点 $x$,其出现的概率是多少。
- 如果 $x$ 是已知确定的,$\theta$ 是变量,这个函数就称为似然函数(likelihood function),它描述对于不同的模型参数,出现 $x$ 这个样本点的概率是多少。
上述的表述看上去似乎在玩文字游戏,但是其实也不难理解,举个抛硬币的例子。
如果抛一枚硬币出现正面的概率是 0.5(参数确定),则抛 10 次硬币,出现 10 次正面的概率是多少呢? $0.5^{10}$ ,这就是概率函数。
如果是抛 10 次硬币出现了 10 次正面,那么什么硬币最可能出现这种情况呢?(参数未知),很明显,硬币不规则,导致出现正面的概率极大,或者说一定会出现正面。这里需要求解的就是抛硬币出现正面的概率。
好了,理解了上述的思想,我们就可以很容易理解最大似然估计,或者说上述的例子其实已经说明了最大似然估计怎么使用。下面对上述抛硬币的例子进行深入解析。
假设有一个造币厂生产某种硬币,现在我们拿到了一枚这种硬币,想试试这硬币是不是均匀的。即想知道抛这枚硬币,正反面出现的概率(记为 $\theta$ )各是多少?
这就是日常中常见的一个需要用统计学习方法解决的实际例子,就是实际日常中,模型的参数往往都是未知的,但是我们可以通过做统计实验得到观察数据。
现在我们拿这枚硬币抛了 10 次,得到的观察数据(记为 $x$ )是:反正正正正反正正正反。我们想求的正面概率。
首先假设模型,记住,最大似然估计是在给定模型的情况下估计参数。抛硬币可以假设是一个二项分布,合情合理。那么,出现实验结果 $x_0$(即反正正正正反正正正反)的似然函数是多少呢?
这里要注意,这里 $f$ 是似然函数, $x$ 是已知量,$\theta$ 是未知量,因此是一个关于 $\theta$ 的函数。最大似然估计,顾名思义就是最大化这个函数,我们可以画出 $f(\theta)$ 的图像:
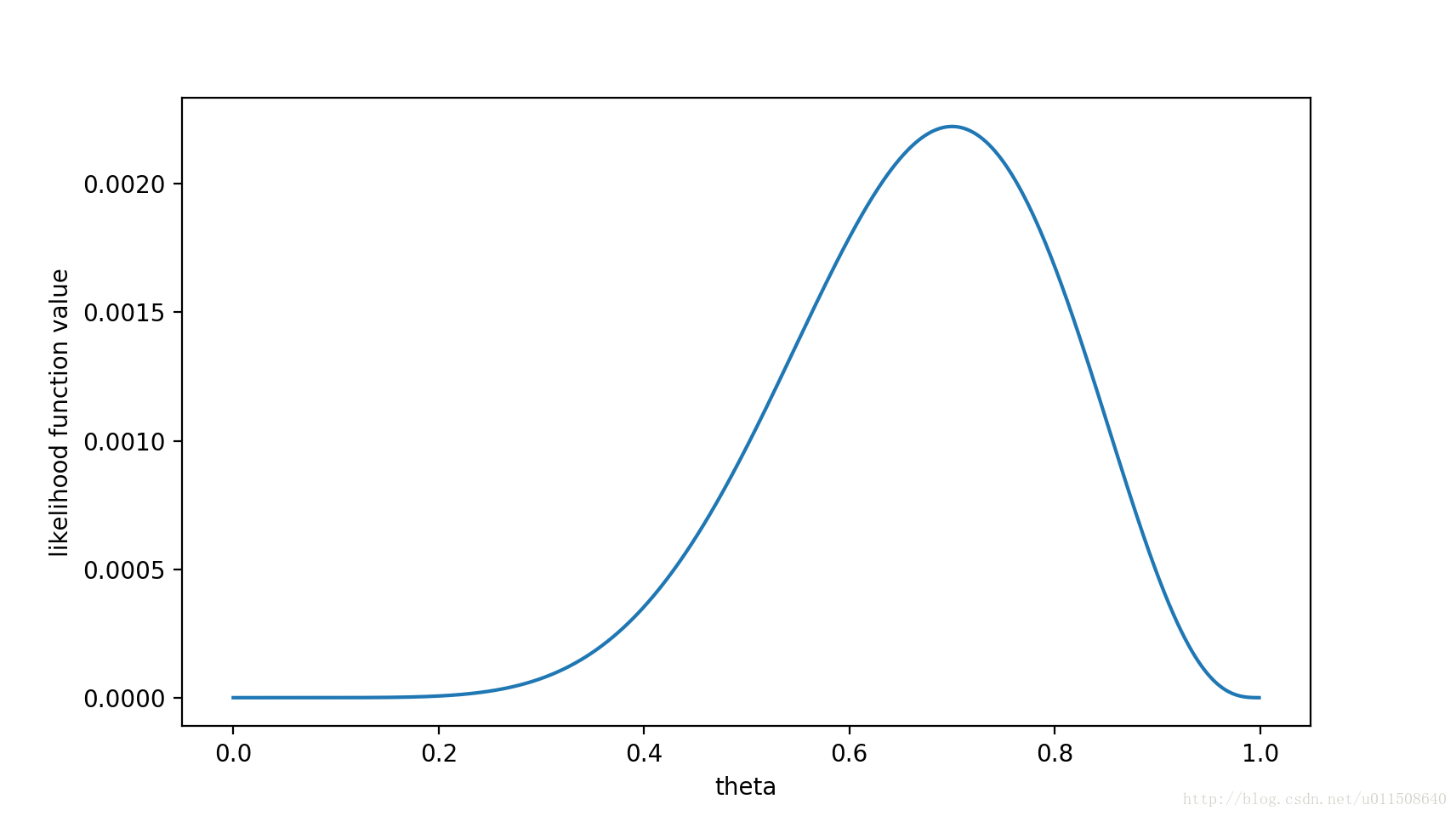
可以看出,在 $\theta=0.7$ 时,似然函数取得最大值。
这样,我们已经完成了对 $\theta$ 的最大似然估计。即抛 10 次硬币,发现 7 次硬币正面向上,最大似然估计认为正面向上的概率是 0.7,看上去也很符合直觉。
且慢,一些人可能会说,硬币一般都是均匀的啊! 就算你做实验发现结果是“反正正正正反正正正反”,我也不信 $\theta = 0.7$,因为 $\theta=0.7$ 这件事本身比 $\theta=0.5$ 这件事更加难以置信。为此,我们就需要引入贝叶斯学派的思想了——要考虑先验概率。 为此,引入了最大后验概率估计(Maximum a posteriori estimation, 简称MAP)。
最大后验概率估计
最大似然估计是单纯根据出现的事件求参数 $\theta$,使似然函数 $P(x|\theta)$ 最大。最大后验概率估计在最大似然估计的基础上,求得的 $\theta$ 不仅仅是让似然函数最大,也让 $\theta$ 自己出现的概率最大。我们可以换个角度来思考这个问题,对于不同的 $\theta$ 可以得到不同的似然函数的值,但是 $\theta$ 本身出现的概率可以用来对似然函数进行正则化,让似然函数更加合理,本身出现概率小的 $\theta$ 会引入惩罚,降低其似然函数的值。但是与损失函数中正则化项一般用加法不同,MAP 里利用乘法引入这个惩罚因子。
MAP 定义是最大化一个函数:
因为 $x$ 是确定的观察事件。因此 $P(x)$ 是已知值,所以可以去掉分母。
假设”投 10 次硬币“是一次实验,实验做了 1000 次,“反正正正正反正正正反”出现了 n 次,则$P(x)=n / 1000$。总之,这是一个可以由实验观察数据集得到的值。
上述的公式是不是很像贝叶斯定理?最大后验概率的名字由来就是最大化 $P(\theta|x)$,这其实是一个后验概率。与似然函数 $P(x|\theta)$ 不同的也仅仅是乘以先验概率 $P(\theta)$。
先验概率我们可以通过假设一个高斯分布来描述。假设 $P(\theta)$ 为均值 0.5,方差 0.1 的高斯函数(万能的假设函数…),如下图:
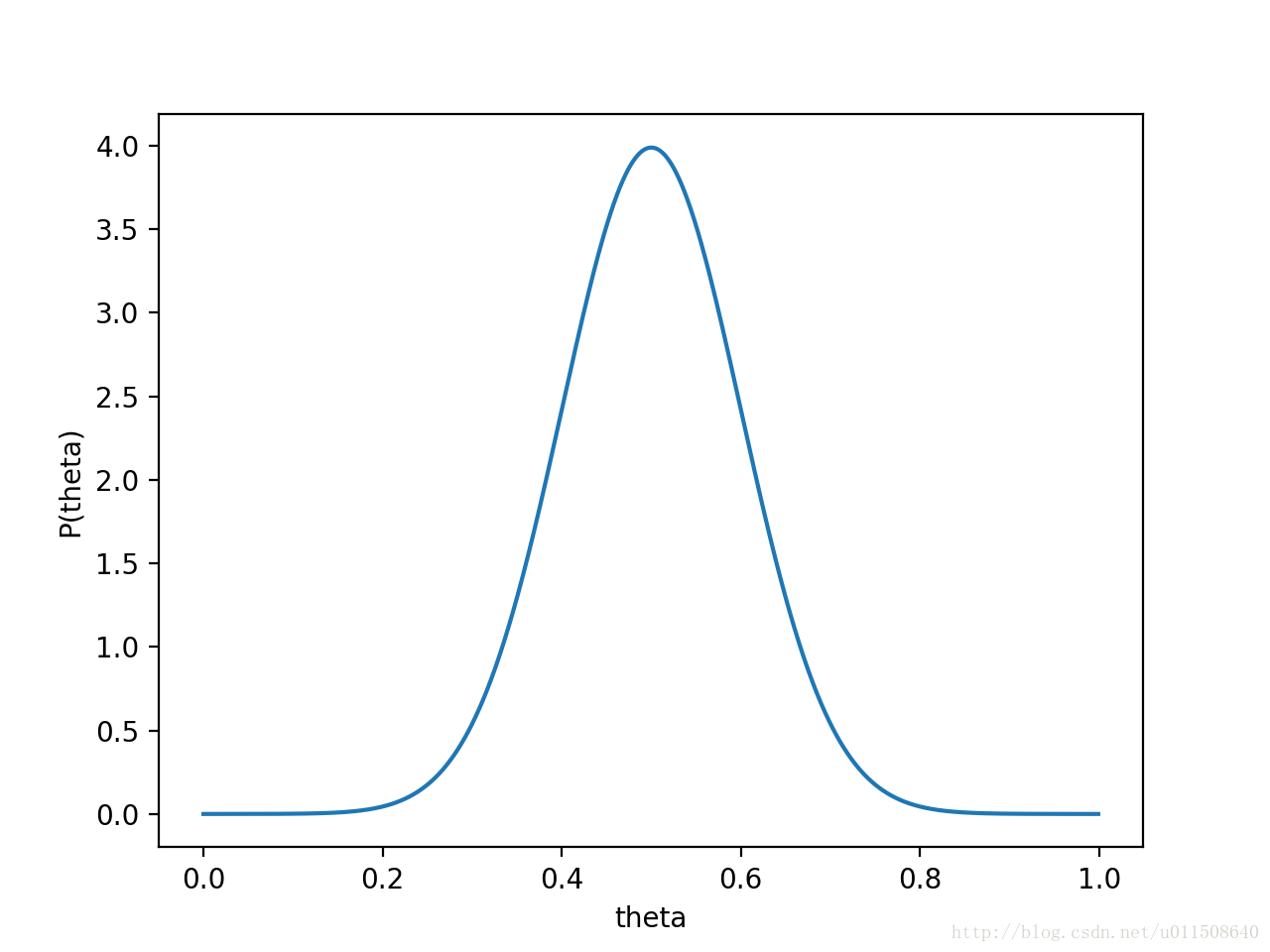
则 $P(x|\theta)P(\theta)$ 的函数图像是:
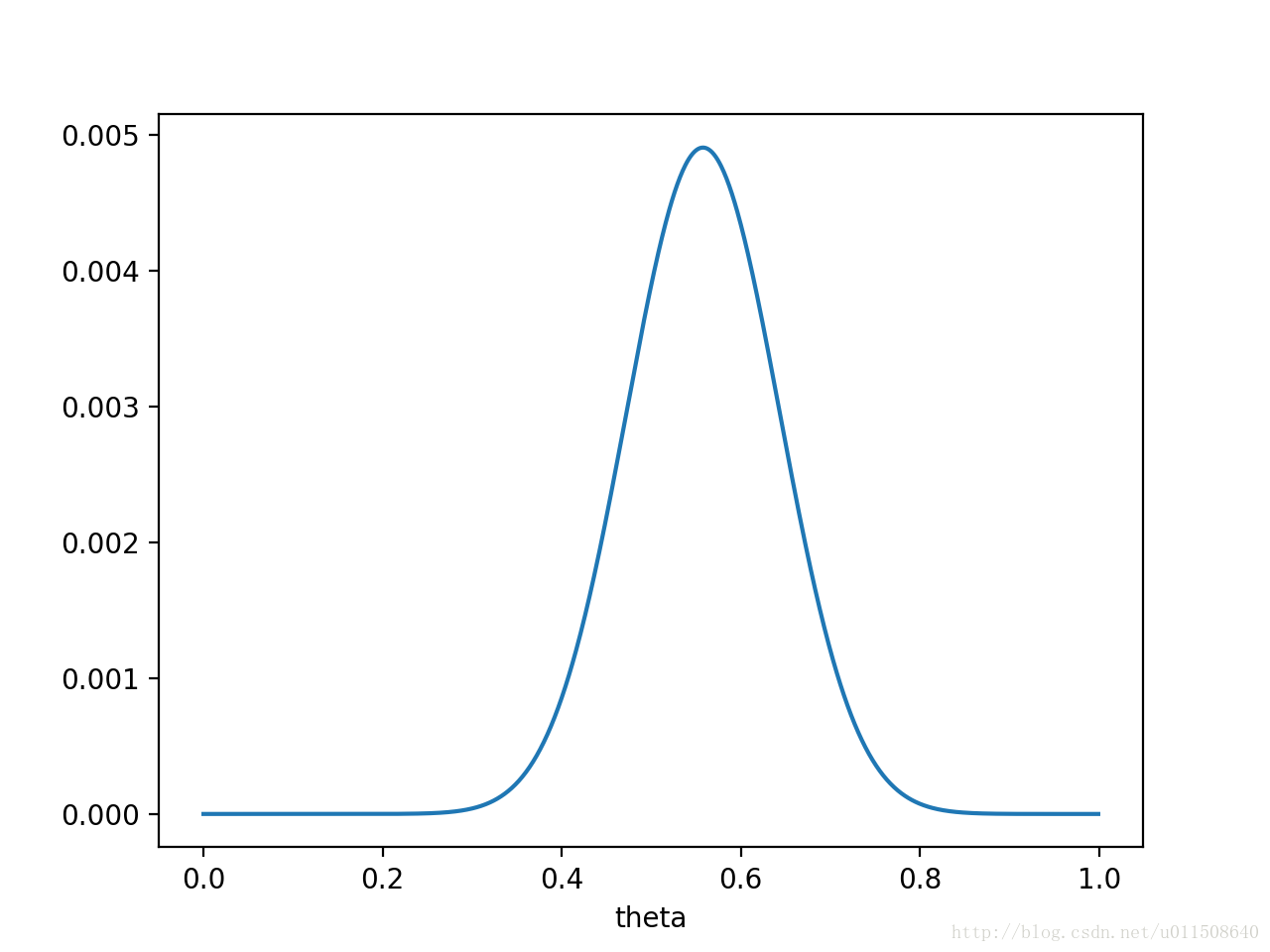
注意,此时函数取最大值时,$\theta$ 取值已向左偏移,不再是 0.7。实际上,在 $\theta=0.558$ 时函数取得了最大值。即用最大后验概率估计,得到 $θ=0.558$ 。最后,那要怎样才能说服一个贝叶斯派相信 $θ=0.7$ 呢?你得多做点实验,让似然函数更加集中。比如做了1000次实验,其中700次都是正面向上,这时似然函数为:
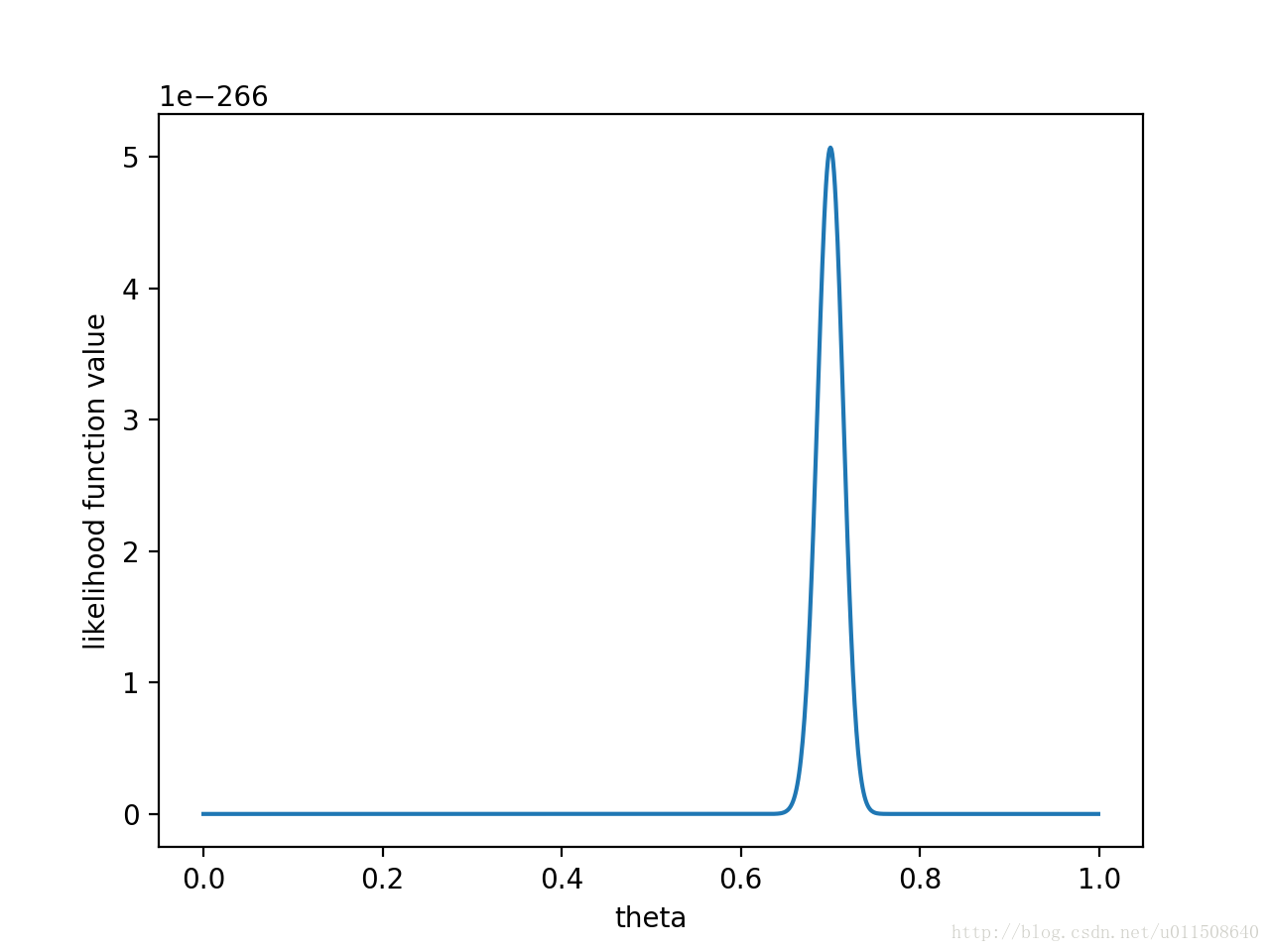
这样即使乘以先验概率的惩罚项,得到的结果还是 $\theta=0.7$ 最大(实际乘的结果是 0.696,如果还不信,继续加大实验次数)。
当然,从我们的计算中可以看出,MAP 是同时受先验概率和似然函数的影响,如果先验概率不合理,比如 $P(\theta=0.7)=0$,那么做多少次实验都没有意义了…