深度学习模型如果想在移动端进行应用,必然面临着计算效率和模型体积的困扰,因此必须进行网络裁剪。本文方法来源于NVIDIA的一篇文章:Pruning Convolutional Neural Networks for Resource Efficient Inference
思路
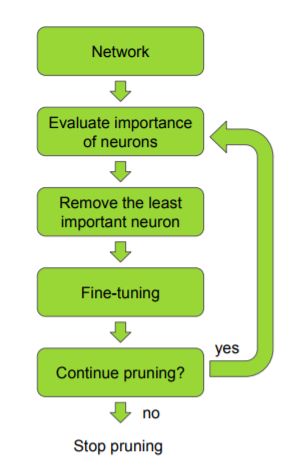
文章的思路很明确,就是在网络模型训练完成之后,对所有的 channel 进行重要性度量,剔除那些对模型精度影响不大的 channel,然后 fine-tune。重复上述的过程,达到裁剪的目的,流程如下:
具体方法
我们可以将网络裁剪看作是一个优化问题:
其中 $D={X={x_0, x_1,…,x_n}, Y={y_0, y_1, …, y_n}}$ 是训练集,$W$ 和 $W’$ 分别为预训练模型参数和剪枝之后的模型参数,作者在 feature map 的基础上作剪枝操作的,上述式子就是在剪枝剩余 $B$ 个 feature maps 的前提下,使剪枝之后的参数模型在训练集的代价函数值和预训练模型在训练集的代价函数值最接近。具体步骤如下:
首先定义一个门函数,要是这个 feature map 需要剪枝的话门函数的值就为 0,否则就为 1,用式子表示就是:
$l$ 代表第 $l$ 层卷积层,$k$ 表示第 $k$ 个channel,因此,剪枝后的模型参数与预训练模型的参数为:
接着就是如何判断一个 channel 的重要性,也就是是否需要被裁剪掉。一个 channel 被剪掉可以表示为: $C(D, h_i=0)$,其中 $h_i=0$ 表示这个 channel 中的参数都为 0,也就是被剪枝掉了。
所以我们所要知道的是一个 channel 被剪枝掉了的影响,也就是:
我们知道,对于函数 $C(D,h_i)$,其泰勒展开表示如下:
其中,$R_1(h_i=0)$ 是拉格朗日余项:
因为它是个很小的数,因此具体计算的时候忽略此项。
因此可得:
其中,$h_i$ 表示卷积核中各个参数,而 $\frac{\partial C}{\partial h_i}$ 表示损失函数对参数求偏导,也就是梯度。所以,通过计算一个卷积核的参数与其梯度的乘积,就能计算该参数对于损失函数的影响。我们对一个 channel 中的参数求平均:
然后归一化:
这样我们就可以得到每个channel对于损失函数的影响力。
实践细节
以下是一些实验过程中的实践经验:
- 在得到每个 channel 的影响力之后,需要判断修剪哪些 channel,可以一次剔除多个,也可以只剔除一个。
- 每次裁剪之后 fine-tune 网络然后再重新修剪。
- 当精度出现明显下降的时候,停止剪枝。
因为泰勒展开和求解影响力引入额外的计算量,因此,一般还需要加入这部分计算量作为正则因子。