SVM 核函数数学原理深入理解

我之前写过一个关于SVM中核函数的基本原理，讲述了核函数的本质是利用高维映射来解决线性不可分的情况。但是具体怎么映射，以及核函数为什么写成两个向量内积的形式还存在一些疑问，这篇文章对这些知识点做一些总结。

感知机的对偶形式

对偶，简单地说，就是从一个不同的角度去解答相似问题，但是问题的解是相通的。或者说原始问题比较难求解，我们去求解另外一个问题，希望通过更简单的方法得到原始问题的解。

《统计学习方法》(李航)在感知机的2.3.3小节中描述了感知机求解的对偶形式：

对偶形式的基本想法是，将\(w\)和\(b\)表示为实例\(x_{i}\)和标记\(y_i\)的线性组合形式，通过求解其系数而求得\(w\)和\(b\)。

对于感知机来说，简单来说，就是用每个样例去的线性加权和去表示要训练得到的\(w\)和\(b\)，最后一次加上去就好了，而我们要学习的参数就从\(w\)和\(b\)转换为了样本的加权系数。这里我就不想再敲一遍公式了，感兴趣的可以看原书的推导过程，这里我贴一张网上的图片：

SVM的对偶形式

和感知机类似，SVM的优化求解也有对偶形式。下面通过SVM求解和求对偶求解的推导来说明。

SVM基本形式求解

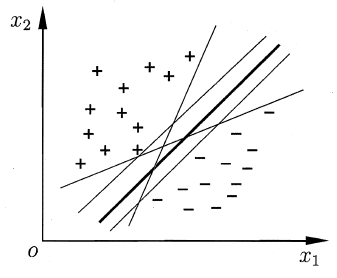
给定一个二分类问题的训练样本集\(D={(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),…,(\boldsymbol{x}_m,y_m)},y_i\in {-1, +1}\)，我们的目标是找到一条分界线/超平面来将两类区分开，如下图：

在样本空间中，超平面可以通过以下线性方程来描述：

$$\boldsymbol{w}^T\boldsymbol{x}+b=0$$

其中，\(\boldsymbol{w}=(w_1,w_2,…,w_d)\)为法向量，决定了超平面的方向；\(b\)为位移项，决定了超平面与原点的距离。如果一个超平面能够将训练样本正确分类，则我们希望这个超平面具有的性质是，对于\((\boldsymbol{x}_i,y_i)\in D\)，有：

$$\boldsymbol{w}^T\boldsymbol{x}+b\left\{ \begin{aligned} \ge0,\ y_i=+1 \\ \le0,\ y_i=-1 \end{aligned} \right.$$

这个式子也是我们在得到超平面之后预测一个新样本的判决条件。

显然，上图中5个超平面都满足要求。但是，哪一个是最好的呢？直观上看，应该去找位于两类训练样本“正中间”的超平面，即上图中最粗的分界线。因为这条线能够在最大程度上容忍两类的数据波动和噪声。因此，为了能够得到“正中间”位置的超平面，我们将上述条件变得更加严格：

$$\boldsymbol{w}^T\boldsymbol{x}+b\left\{ \begin{aligned} \ge+1,\ y_i=+1 \\ \le-1,\ y_i=-1 \end{aligned} \right. \qquad(1)$$

显然，条件严格后，靠近样本边缘的一些超平面可能会不符合要求，最后会剩下比较靠中间的几个超平面。那么，如何选出最“正中间”的那个超平面呢？我们可以给一个具体的量化目标：让超平面与最近的样本的距离最大。

如下图所示，距离超平面最近的这几个样本点可以使得公式 (1) 的等号成立，它们被称为“支持向量”（Support Vector）。

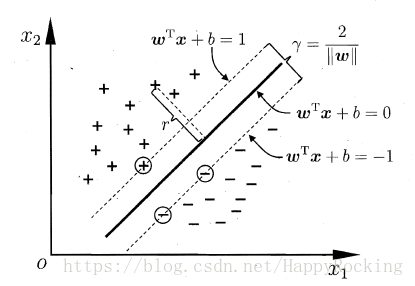
样本空间中任意点\(\boldsymbol{x}\)到超平面的距离的计算公式为：

$$r=\frac{|\boldsymbol{w}^T\boldsymbol{x}+b|}{||\boldsymbol{w}||}$$

因此，两类的支持向量到超平面的距离之和为\(\frac{2}{\boldsymbol{w}}\)，这就是“间隔”（margin）

如果想找到具有“最大间隔”（maximum margin）的超平面，那么需要最小化\(||\boldsymbol{w}||^2\)。因此，最后需要求解的问题为：

$$\max_{\boldsymbol{w},b} \quad \frac{1}{2}||\boldsymbol{w}||^2 \\ s.t. \quad y_i(\boldsymbol{w}^T\boldsymbol{x}+b)\ge1,\quad i=1,2,...,m \\$$

这就是支持向量机（Support Vector Machine,SVM）的基本型。

SVM对偶形式求解

我们希望求解问题(2)来得到“正中间”的分界超平面：

$$f(\boldsymbol x)={\boldsymbol w}^T\boldsymbol x + b$$

其中，\(\boldsymbol w\)和\(b\)正式模型的最优解的参数。问题(2)本身是一个凸二次规划问题，可以直接使用现成的优化计算包求解。但我们有更高效的办法，即转为求解其对偶问题，转换过程如下。（下面的推导我自己也看的有点蒙，看不懂略过吧）

根据拉格朗日乘子法，对原问题的每条约束添加拉格朗日乘子\(\alpha \ge0\)，则该问题的拉格朗日函数可写为：

$$L(\boldsymbol w,b,\boldsymbol\alpha)=\frac1 2 ||\boldsymbol w||^T+\sum_{i=1}^{m}\alpha_i[1-y_i(\boldsymbol w^T\boldsymbol x_i+b)]\quad(3)$$

其中，\(\boldsymbol\alpha=(\alpha_1,\alpha_2,…,\alpha_m)\)。可以发现：

$$\alpha_i[1-y_i(\boldsymbol w^T\boldsymbol x_i+b)]\le0$$

所以\(L(\boldsymbol w,b,\boldsymbol\alpha)\le \frac1 2 ||\boldsymbol w||^T\)，即拉格朗日函数是原问题的一个下界。我们要想找到最接近原问题最优值的一个下界，就需要求出下界的最大值。

根据拉格朗日对偶性，原始问题的对偶问题是最大化最小问题：

$$\max_\alpha \min_{\boldsymbol{w},b}L(\boldsymbol w,b,\boldsymbol\alpha)$$

首先，求\(\min_{\boldsymbol{w},b}L(\boldsymbol w,b,\boldsymbol\alpha)\)，消除掉\(\boldsymbol w, b\)偏导为0，可推出：

$$\begin{aligned} \frac{\partial L}{\partial \boldsymbol w}&=\boldsymbol w + \sum_{i=1}^m \alpha_i(-y_i \boldsymbol x_i)=0 \ \Rightarrow \boldsymbol w=\sum_{i=1}^m \alpha_i y_i \boldsymbol x_i\quad(4) \\ \frac{\partial L}{\partial \boldsymbol w}&= -\sum_{i=1}^m \alpha_i y_i=0 \qquad\quad\ \ \ \Rightarrow \sum_{i=1}^m \alpha_i y_i=0\ \quad(5) \end{aligned}$$

将公式(4)和(5)带入到拉格朗日函数(3)，得到：

$$\begin{aligned} L(\boldsymbol w,b,\boldsymbol\alpha) &=\frac1 2 ||\boldsymbol w||^T+\sum_{i=1}^{m}\alpha_i[1-y_i(\boldsymbol w^T\boldsymbol x_i+b)] \\ &=\frac1 2 \boldsymbol w^T\boldsymbol w +\sum_{i=1}^m\alpha_i -\sum_{i=1}^m\alpha_iy_i\boldsymbol x_i^T\boldsymbol w-\sum_{i=1}^m\alpha_iy_ib \\ &= \frac 1 2\boldsymbol w^T \boldsymbol w+\sum_{i=1}^m\alpha_i-\boldsymbol w^T\boldsymbol w-0 \\ &=\sum_{i=1}^m\alpha_i-\frac1 2 \sum_{i=1}^m\sum_{j=1}^m \alpha_i\alpha_jy_iy_j\boldsymbol x_i^T\boldsymbol x_j^T \end{aligned}$$

因此，问题（2）的对偶问题是：

$$\begin{aligned} \max_\alpha\quad &\sum_{i=1}^m\alpha_i-\frac1 2 \sum_{i=1}^m\sum_{j=1}^m \alpha_i\alpha_jy_iy_j\boldsymbol x_i^T\boldsymbol x_j^T\quad(6) \\ s.t.\quad&\sum_{i=1}^T\alpha_iy_i=0 &\alpha_i\ge0,i=1,2,...,m. \end{aligned}$$

解出\(\boldsymbol \alpha\)后，便可以求出\(\boldsymbol w\)和\(b\)，即可得到模型：

$$\begin{aligned} f(\boldsymbol x)&=\boldsymbol w^T\boldsymbol x + b \\ &=\sum_{i=1}^m\alpha_iy_i\boldsymbol x_i^T\boldsymbol x+b \end{aligned}$$

需要注意的是，问题（2）有不等式约束，因此对偶问题需要满足KKT条件：

$$\left\{ \begin{aligned} &\alpha_i\ge0 \\ &y_if(\boldsymbol x_i)-1\ge0 \\ &\alpha_i(y_if(\boldsymbol x_i)-1)=0 \end{aligned} \right.$$

因此，对于训练样本\((\boldsymbol x_i,y_i)\)，总有\(\alpha_i=0\)或者\(y_if(\boldsymbol x_i)=1\)。若\(\alpha_i=0\)则该样本不会对\(f(\boldsymbol x)\)的值有任何影响；若\(\alpha_i>0\)，则必有\(y_if(\boldsymbol x_i)=1\)，所对应的样本点位于最大间隔边界上，是一个支持向量。这显示出支持向量的一个重要性质：训练完成后，大部分的训练样本都不需要保留，最终模型仅与支持向量有关。

简单总结：

和感知机的对偶求解类似，SVM也是通过样本的线性加权和来求解\(\boldsymbol w\)和\(b\)，进而得到SVM的最优解。我们注意到，在利用对偶求解的过程中，是要利用两个样本的内积来求解的，这就为核函数的使用埋下了伏笔。

SVM核函数

上一小节讲的是线性可分的情况下，SVM的超平面求解。如果样本在特征空间内线性不可分，则需要利用核函数将其映射到高维空间中，让其在高维空间中线性可分。根据SVM基础形式的求解，我们可能会想到下面的方式：

$$f(\boldsymbol x)=\sum_{i=1}^{N} w_i \phi_i(\boldsymbol x)+b$$

这里的\(\phi_i())就是从输入的特征空间到某个更高维的特征空间的映射，这就意味着建议了非线性的学习器分为两步：

1. 首先使用一个非线性映射将数据变换到另一个特征空间
2. 在高维的特征空间中使用线性学习器分类

这种基本型的求解是非常难的，因为这个映射函数是非常难以寻找和求解的！（据说NP难），而了解了SVM的对偶形式给了另一种求解思路：

$$f(\boldsymbol x)=\sum_{i=1}^{l} \alpha_i y_i \left \langle \boldsymbol \phi_i(\boldsymbol x_i) \cdot \boldsymbol \phi(\boldsymbol x) \right \rangle + b$$

注意到，我们在求解的时候需要计算\(\boldsymbol \phi_i(\boldsymbol x_i) \cdot \boldsymbol \phi(\boldsymbol x)\)，也就是映射后的两个样本的高维特征的内积形式，如果有一种方法可以在特征空间中直接计算这个东西，是不是就很方便了？对的，核函数就是做这个的：

$$K(\boldsymbol x, \boldsymbol z) = \boldsymbol \phi(\boldsymbol z) \cdot \boldsymbol \phi(\boldsymbol x)$$

上述的思想就是SVM核函数的核心思想，以前一直没太明白核函数为啥是映射两个样本的内积，直到看到对偶形式的求解才明白。有了这个概念，再去阅读核函数的原理就恍然大悟了。下面以多项式核函数和高斯核来具体看看核函数是如何映射的。

多项式核函数

对于一个多项式核函数

$$K(\boldsymbol x, \boldsymbol z) = (\boldsymbol x^T \boldsymbol z)^2$$

假设每个向量的维度为2，也就是： \(\boldsymbol x=(x_1, x_2), \boldsymbol z=(z_1,z_2)\)，则有：

$$K(\boldsymbol x, \boldsymbol z) = (x_1z_1 + x_2z_2)^2 = x_1^2+y_1^2+2x_1x_2y_1y_2 + x_2^2y_2^2$$

又因为特征映射为：

$$K(\boldsymbol x, \boldsymbol z) = \boldsymbol \phi(x)\boldsymbol \phi(z)$$

所以可得：

$$\boldsymbol \phi(x) = (x_1^2, \sqrt{2}x_1^2x_2^2, x_2^2)$$

可以看出，将\(\boldsymbol R^2\)映射到了\(\boldsymbol R^3\)

高斯核

现在分析高斯核：

$$K(\boldsymbol x, \boldsymbol z) = exp(-||x-y||^2)$$

和上面一样，假设每个向量有两个维度，则高斯核展开为：

$$\begin{aligned} K(\boldsymbol x, \boldsymbol z) &= exp(-|\boldsymbol x^2-\boldsymbol z^2|) \\ &= exp(-(x_1^2-z_1^2)-(x_2^2-z_2^2)) \\ &= exp(-x_1^2+2x_1z_1-z_1^2-x_2^2+2x_2z_2-z_2^2) \\ &= exp(-|\boldsymbol x|^2)exp(-|\boldsymbol z|^2)exp(2\boldsymbol x \boldsymbol z) \end{aligned}$$

根据泰勒展开式：

$$e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}$$

所以可得核函数的展开为：

$$K(\boldsymbol x, \boldsymbol z) = exp(-||\boldsymbol x||^2)exp(-||\boldsymbol z||^2) \sum_{n=0}^{\infty}\frac{(2\boldsymbol x^T\boldsymbol y)^n}{n!}$$

因此，高斯核函数是将变量从现有的特征空间映射到无限维的特征空间中。