在MXNe t框架学习(1)中,我们介绍了一些有关MXNet的安装和基础知识,并介绍了NDArray API(简而言之:NDArrays可用于存储数据、参数等信息)。在介绍过数据的存储后,本文将谈谈MXNet定义计算步骤的方式。
1. 数据流编程
symbol 可以说是 MXNet 最重要的一部分API了,主要定义了计算流程。在此之前,我觉得有必要说一下不同的编程方式:
我们都知道那个著名的公式:“程序=数据结构+代码(算法)”。在MXNet中,NDArrays是数据结构,那么接下来需要写代码(算法)了,所谓的代码或者算法其实就是如何指导计算机来进行一步步的计算。
对于绝大多数情况下的编程,我们需要明确定义所有步骤,随后针对数据按顺序运行。这也叫“指令式编程(Imperative programming)”,Fortran、Pascal、C、C++等都是这样做的,这么做也没什么错。
然而神经网络从本质上来说是一种并行的结构:在特定的技术层中,所有输出都可同步计算。每个层也可以并行运行。因此为了获得最佳性能,我们必须使用多线程或其他类似机制自行实现并行处理。具体做法大概都知道,而就算写出了恰当的代码,如果数据规模或网络布局不断变化,如何确保能可复用地进行?好在还有其他备选方案。
数据流编程(Dataflow programming)是一种定义并行运算的灵活方法,这种方法中,数据可通过图(Graph)的方式流动。Graph定义了运算顺序,即数据是要按顺序运算或并行运算。每个运算都是一种黑匣子:我们只需要为其定义输入和输出,无需制定具体的行为。
按照传统的计算机科学思路来看,这似乎很不靠谱,但实际上神经网络就是通过这种方式定义的:输入的数据流进行一系列叫做“层(Layer)”的有序操作,每一层可以并行运行指令。MXNet和Tensorflow都是这种计算方式。
说的差不多了,一起看一个例子吧。我们可以通过下列方式将E定义为(A*B) + (C*D)。
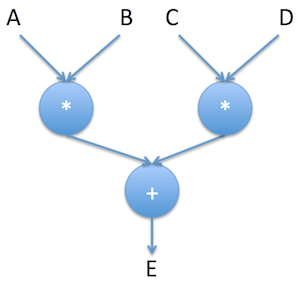
1 | E = (A\*B) + (C\*D) |
A、B、C、D具体是什么目前暂不重要,它们实际上是符号(Symbol)。
无论输入了什么内容(整数、向量、矩阵等),这个Graph可以告诉我们如何通过计算获得输出值,但前提是必须定义了“+”和“*”操作。
这个Graph还可以告诉我们 (A*B) 和 (C*D) 可以并行运算。
当然,MXNet会通过这些信息进行并行优化。
2. Symbol模块
2.1 Symbol API
至此已经了解到这些东西为何叫做符号(Symbol)(显而易见嘛!)接下来一起看看如何为上述例子编写代码。1
2
3
4
5
6import mxnet as mx
a = mx.symbol.Variable('A')
b = mx.symbol.Variable('B')
c = mx.symbol.Variable('C')
d = mx.symbol.Variable('D')
e = (a*b)+(c*d)
看到了吗?上述代码完全是有效的。我们可以直接向E指派结果,而无需知道A、B、C、D分别是什么。继续吧。1
2
3
4
5
6(a,b,c,d)
(<Symbol A>, <Symbol B>, <Symbol C>, <Symbol D>)
e
<Symbol _plus1>
type(e)
<class 'mxnet.symbol.Symbol'>
A、B、C、D是我们明确声明的符号。但E略有不同,它也是符号,但实际上它是“+”运算的结果。接下来进一步看看E。1
2
3
4
5
6e.list_arguments()
['A', 'B', 'C', 'D']
e.list_outputs()
['_plus1_output']
e.get_internals().list_outputs()
['A', 'B', '_mul0_output', 'C', 'D', '_mul1_output', '_plus1_output']
从上述代码可以知道:E取决于变量A、B、C、D,用于计算E的是一次求和操作,E实际上就是 (a*b)+(c*d) 的结果。当然,通过使用符号,我们能做的远远不止“+”和“*”。与NDArrays类似,还可以定义很多不同类型的运算(数学、格式等)。详细信息可以参阅API 文档。
至此我们已经了解了如何定义计算步骤。接下来看看如何将其应用给实际数据。
2.2 NDArray与Symbol的绑定
将Symbol定义的计算步骤应用给NDArray中存储的数据,需要一种名为“绑定(Binding)”的操作,例如将一个NDArray分配给Graph的每个输入变量。
继续用上面的例子来看。在这里我们将“A”设置为1,“B”为2,“C”为3,“D”为4,因此我创建了4个包含单一整数的NDArray。1
2
3
4
5import numpy as np
a_data = mx.nd.array([1], dtype=np.int32)
b_data = mx.nd.array([2], dtype=np.int32)
c_data = mx.nd.array([3], dtype=np.int32)
d_data = mx.nd.array([4], dtype=np.int32)
随后将每个NDArray绑定给对应的Symbol。这里请注意,还需要选择用于执行该操作的上下文(CPU或GPU)。1
2
3executor=e.bind(mx.cpu(), {'A':a_data, 'B':b_data, 'C':c_data, 'D':d_data})
executor
<mxnet.executor.Executor object at 0x10da6ec90>
接着需要让输入的数据流经Graph并获得结果:这是通过forward()函数实现的。由于一个Graph可以包含多个输出,因此该函数可以返回NDArrays组成的数组。这里我们只有一个输出,即“14”这个值,这个值当然与 (12)+(34) 的运算结果是相等的。
1 | e_data = executor.forward() |
接下来我们将这个Graph应用给四个1000x1000矩阵,这些矩阵中填充了介于0和1之间的随机浮点数。为此我们只需要定义新的输入数据,绑定和计算过程是完全相同的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24a_data = mx.nd.uniform(low=0, high=1, shape=(1000,1000))
b_data = mx.nd.uniform(low=0, high=1, shape=(1000,1000))
c_data = mx.nd.uniform(low=0, high=1, shape=(1000,1000))
d_data = mx.nd.uniform(low=0, high=1, shape=(1000,1000))
executor=e.bind(mx.cpu(), {'A':a_data, 'B':b_data, 'C':c_data, 'D':d_data})
e_data = executor.forward()
e_data
[<NDArray 1000x1000 @cpu(0)>]
e_data[0]
<NDArray 1000x1000 @cpu(0)>
e_data[0].asnumpy()
array([[ 0.89252722, 0.46442914, 0.44864511, ..., 0.08874825,
0.83029556, 1.15613985],
[ 0.10265817, 0.22077513, 0.36850023, ..., 0.36564362,
0.98767519, 0.57575727],
[ 0.24852338, 0.6468209 , 0.25207704, ..., 1.48333383,
0.1183901 , 0.70523977],
...,
[ 0.85037285, 0.21420079, 1.21267629, ..., 0.35427764,
0.43418071, 1.12958288],
[ 0.14908466, 0.03095067, 0.19960476, ..., 1.13549757,
0.22000578, 0.16202438],
[ 0.47174677, 0.19318949, 0.05837669, ..., 0.06060726,
1.01848066, 0.48173574]], dtype=float32)
很酷吧!这种数据和计算之间明确的区分使得我们可以在不同环节同时获得最佳效果:
我们可以使用自己已经很熟悉的指令式编程模式加载和准备数据,甚至可以在这个过程中使用外部库(整个过程和传统变成方式完全相同)。计算过程则使用符号式编程方式进行,借此MXNet不仅可以实现代码与数据的解耦,而且可以随着Graph的优化实现并行执行。