B树以及B+树

MySQL数据库使用B+树作为索引存储的数据结构，B+树是从B-Tree发展而来，本文对该数据结构进行了详细解析。

1. B-Tree

B树等于B-树，不是二叉搜索树，实际上没有B-树的说法，而BST和B树不一样

引自wiki：

B树（英语：B-tree）是一种自平衡的树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数时间内完成。B树，概括来说是一个一般化的二叉查找树（binary search tree），可以拥有多于2个子节点。与自平衡二叉查找树不同，B树为系统大块数据的读写操作做了优化。B树减少定位记录时所经历的中间过程，从而加快存取速度。B树这种数据结构可以用来描述外部存储。这种数据结构常被应用在数据库和文件系统的实现上。

B 树（B-Tree）是为磁盘等辅助存取设备设计的一种平衡查找树，它实现了以 O(log n) 时间复杂度执行查找、顺序读取、插入和删除操作。由于 B 树和 B 树的变种在降低磁盘 I/O 操作次数方面表现优异，所以经常用于设计文件系统和数据库。

如下图是一棵键值为英语字母的 B 树，带浅阴影的节点是查找字母 R 时要检查的节点。

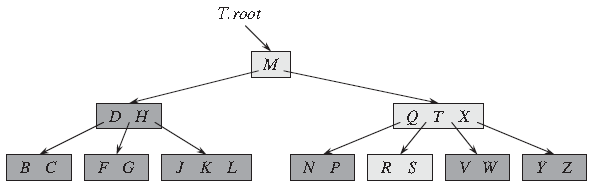
可以发现，上述的查找过程和BST的查找过程很相似。下面对B-Tree中的节点关系做一些说明，这个和BST有一些不同。

B树内的节点关系

B 树中的节点分为内部节点（Internal Node）和叶节点（Leaf Node），内部节点也就是非叶节点（Non-Leaf Node）。

B 树的内部节点可以包含 2 个以上的子节点，所以在设计时可以预先设定可包含子节点的数量范围，也就是上界（Upper Bound）和下界（Lower Bound）。当向节点插入或删除数据时，也就意味着子节点的数量发生变化。为了维持在预先设定的数量范围，内部节点可能会被合并（Join）或拆分（Split）。因为子节点的数量有一定的范围，所以 B 树不需要频繁地变化以保持平衡（提高了效率）。但同时，由于节点可能没有被完全填充，所以会浪费一些空间。

B 树中每一个内部节点会包含一定数量的键值（Key）。这些键值同时也扮演着分割子节点的角色。例如，假设某内部节点包含 3 个子节点，则实际上必须有 2 个键值：a1 和 a2。其中，a1 的左子树上的所有的值都要小于 a1，在 a1 和 a2 之间的子树中的值都大于 a1 并小于 a2，a2 的右子树上的所有的值都大于 a2。

通常，键值的数量被设定在 d 和 2d 之间，其中 d 是可包含键值的最小数量。可知，d + 1 是节点可拥有子节点的最小数量，也就是树的最小的度（Degree）。因数 2 将确保节点可以被合并或拆分。

• 如果一个内部节点有 2d 个键值，那么添加一个键值给该节点将会导致 2d + 1 的数量大于范围上界，则会拆分 2d + 1 数量的节点为 2 个 d 数量的节点，并有 1 个键值提升至父节点中。

• 类似地，如果一个内部节点和它的邻居节点（Neighbor）都包含 d 个键值，那么删除一个键值将导致此节点拥有 d - 1 个键值，小于范围下界，则会导致与邻居节点合并。合并后的节点包括 d – 1 的数量加上邻居的 d 的数量和两者的父节点中的 1 个键值，共为 d – 1 + d + 1 = 2d 数量的节点。

深度（Depth）描述树中层（Level）的数量。B 树通过要求所有叶节点保持在相同深度来保持树的平衡。深度通常会随着键值的不断添加而缓慢地增长。

B树的定义

对于 B 树定义中的一些术语常有混淆，比如对于阶（Order）的定义。Knuth Donald 在 1998 年将阶（Order）定义为节点包含子节点的最大数量。

使用阶来定义 B 树，一棵 m 阶的 B 树，需要满足下列条件：

• 每个节点最多包含 m 个子节点。
• 除根节点外，每个非叶节点至少包含 m/2 个子节点。
• 如果根节点包含子节点，则至少包含 2 个子节点。
• 拥有 k 个子节点的非叶节点将包含 k - 1 个键值。
• 所有叶节点都在同一层中。

下面是一棵高度（Height）为 3 的 B 树：

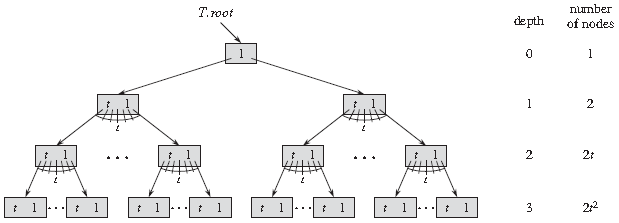
B 树上大部分操作所需的磁盘存取次数与 B 树的高度成正比。

• h 代表 B 树的高度；
• n 代表整个树中包含键值的数量 n > 0；
• m 为内部节点可包含子节点的最大数量，则当树满时 n = mh – 1；每个内部节点最多包含 m - 1 个键值；
• d 代表内部节点可包含最少子节点的数量，即最小度数（Degree）有 d = ⌈m/2⌉。

B 树的最优条件下的 h 为：

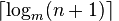
B 树的最差条件下的 h 为：

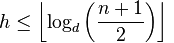
B 树的操作

• 查询操作

  在 B 树中查询键值与在二叉树中的键值查询方式是类似的。从根节点开始查询，通过递归进行自顶向下的遍历。在每一层上，将查询键值与内部节点中的键值比较，以确定向哪个子树中进行遍历。

![img](/images/posts/mysql/btree/B-Tree-query.png)

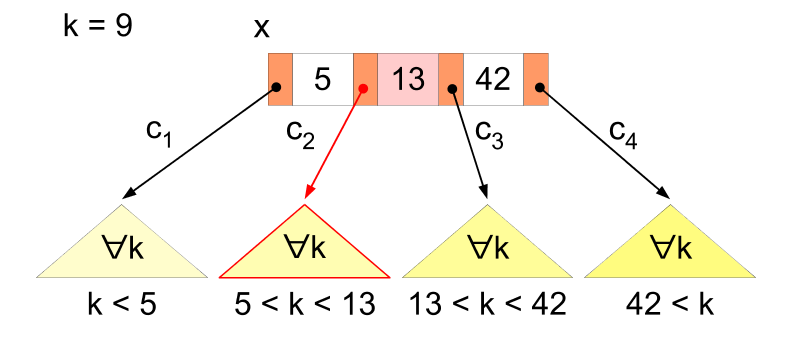
• 插入操作

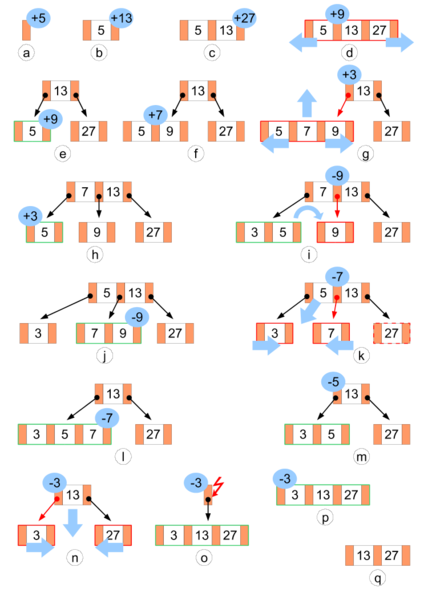
  当要插入一个新的键值时，首先在树中找到该键值应当被插入的叶节点的位置：

  • 如果叶节点包含键值的数量在设定的范围上界和下界内，则直接插入新键值，并保持键值在节点中顺序。

  • 否则，节点已满，将节点分割为 2 个节点：

    1. 选择中间值（Median）作为分割点；
    2. 小于中间值的键值放入新的左节点中，大于中间值的键值放入新的右节点中；
    3. 将中间值插入到父节点中。此时可能导致父节点满，采用同样方式分割。如果父节点不存在，比如是根节点，则创建一个新的父节点，也就导致树的高度增长。

    ![img](/images/posts/mysql/btree/B-Tree-insert.png)

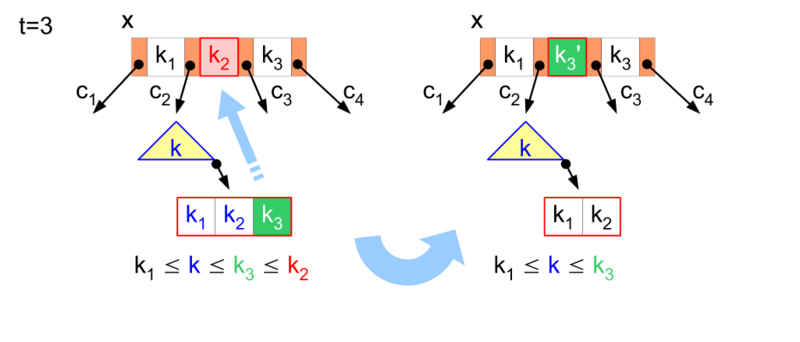
• 删除操作

  在 B 树中删除键值可以通过不同的策略来实现，这里介绍常见的定位删除策略：定位键值后删除，然后重构整个树至平衡。平衡指的是仍然保持 B 树的性质。

  1. 搜索要被删除键值的位置。
  2. 如果键值在叶节点中，则直接删除。
  3. 如果键值在内部节点中，由于其正扮演分割子节点的角色，所以删除后需要找一个替代键值继续保持两个子节点的分割。此时，可以选择左子节点中最大的键值，或者右子节点中最小的键值。将选中的键值从子节点中删除，然后插入到被替换的位置。
  4. 如果删除键值后的节点已经不满足对最少键值数量的要求，则需要重平衡整棵树，平衡操作包括旋转（Rotation）、组合（Join）等。

![img](/images/posts/mysql/btree/B-Tree-delete.png)

2. B 树的变种

“B 树” 这个术语在实际应用中还代表着多种 B 树的变种，它们有着相似的结构，却各有特点和优势：

• B 树在其内部节点中存储的键值不会再在叶节点中存储，内部节点不仅存储键值也会存储键值关联附属数据，或者存储指向关联附属数据的指针。同时，B 树会保持内部节点的 1/2 填充。

• B+ 树是 B 树的一个变种，在内部节点中存储的键值同样也会出现在叶节点中，但内部节点中不存储关联附属数据或指针。在叶节点中的不仅存储键值，还存储关联附属数据或指针。此外，叶节点还增加了一个指向下一个顺序关联叶节点的指针，以改进顺序读取的速度。

• B* 树也是 B 树的一个变种，要求除根节点外的内部节点要至少 2/3 填充，而不是 1/2 填充。为了维持这样的结构，当一个节点填满后不会立即分割节点，而是将它的键值与下一个节点共享，当两个节点都填满之后，再将 2 个节点分割成 3 个节点。

3. B+ 树的优势

B+ 树是 B 树的一个变种，在内部节点中存储的键值同样也会出现在叶节点中，但内部节点中不存储关联附属数据或指针。在叶节点中的不仅存储键值，还存储关联附属数据或指针。这样，所有的附属数据都保存在了叶节点中，只将键值和子女指针保存在了内节点中，因此最大化了内节点的分支能力。此外，叶节点还增加了一个指向下一个顺序关联叶节点的指针，以改进顺序读取的速度。

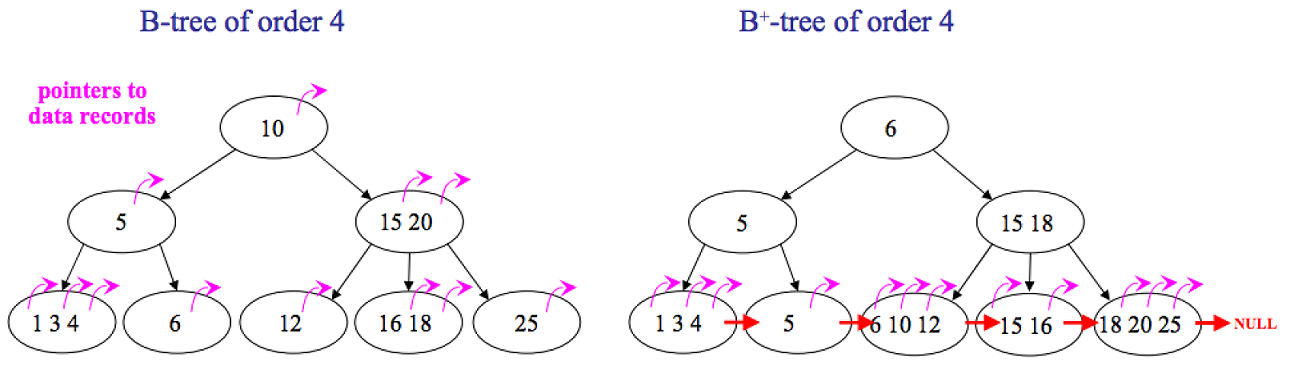
常见的文件系统和数据库均使用 B+ 树实现，例如：

• 文件系统：NTFS, ReiserFS, NSS, XFS, JFS, ReFS, BFS, Ext4；
• 关系型数据库：DB2, Informix, SQL Server, Oracle, Sybase ASE, SQLite；
• NoSQL 数据库：CouchDB, Tokyo Cabinet；

B+ 树的优势在于：

• 由于内部节点不存储键值关联的附属数据，所以内部节点节省的空间可以存放更多的键值。也就意味着从磁盘存取一页时可获得更多的键值信息。
• 叶节点形成了一个链，所以对树的全扫描就是对所有叶节点的线性遍历。