0%

ROI Align和图像的双线性内插法

发表于 更新于 分类于 阅读次数：
本文字数： 1.6k 阅读时长 ≈ 3 分钟

最近在看Mask R-CNN，了解到其边框包裹紧密的原因在于将 Roi Pooling 层替换成了 RoiAlign 层，后者舍去了近似像素取整数的量化方法，改用双线性插值的方法确定特征图坐标对应于原图中的像素位置。本文整理了双线性插值的一些知识，便于更好的理解其中的操作。

线性插值

学过初中几何的学生都知道，二维直角坐标系中，已知两个点(x1, y1)和(x2, y2)，可以确定一条直线方程，对于给定的一个x，介于x1和x2之间，可以求得其满足直线方程的y：

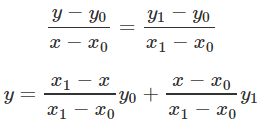
这个应该很好理解，就是计算x分别和x1，x2的距离作为一个权重，用于对y1和y2的加权。

双线性插值

双线性插值本质上就是在两个方向上做线性插值。

在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

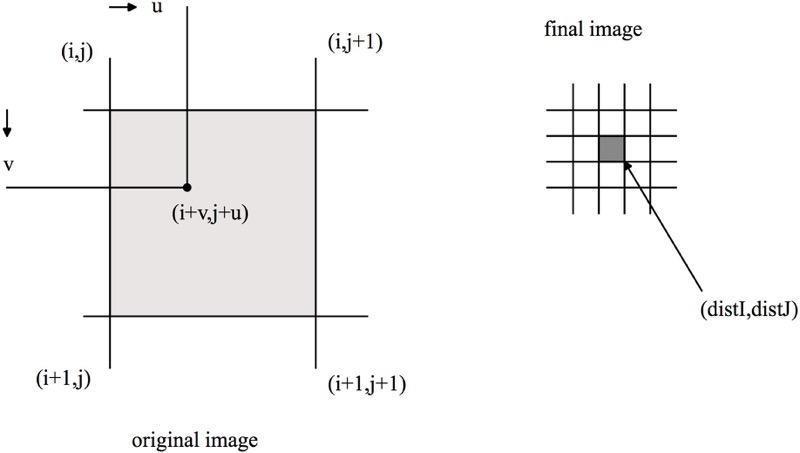
对于双线性插值，其要插值的像素和原图中周围四个像素有关，然后根据与这些像素的距离来进行像素值的加权计算。

简单分析如下：

  • 目标插值图中的某像素点(distI, distJ)在原图中的映射为(i + v, j + u)

    • 这个映射关系是根据图像缩放后的比例来确定的

    • 0 < v, u < 1

  • (i + v, j + u)处值的计算就是邻近4个像素点的分别在x轴和y轴的权值和

插值公式

  • 设f(i, j)为(i, j)坐标点的值（灰度值）

  • u为列方向的偏差

  • v为行方向的偏差

那么插值公式如下（最终F(i + v, j + u)处的实际值）

1
2
3
4
5
f(i + v, j + u) = partV + partV1;

partV = v * ((1 - u) * f(i + 1, j) + u * f(i + 1, j + 1));

partV1 = (1 - v) * ((1 - u) * f(i, j) + u * f(i, j + 1));

或展开为：

1
f(i + v, j + u) = f(0, 0)(1 - v)(1 - u) + f(0, 1)(1 - v)(u) + f(1, 0)(v)(1 - u) + f(1, 1)(v)(u)

上式中，分别是四个坐标点对x和y方向进行插值，简单的说：

  • u越接近0，(i, j)与(i + 1, j)的权值越大

  • v越接近0，(i, j)与(i, j + 1)的权值越大

双线性内插法常用于图像的缩放。

ROI Align

ROI Pooling存在的问题

熟悉ROI Pooling的都知道，这一操作存在两次取整过程：

  • 首先是原图和特征图之间比例缩放，比如VGG16最后一层是原图的1/16，如果某个候选区域的大小在原图上是 211*223，则长与宽除不尽，需要取整，得到其在特征图大小为：211/16≈13，223/16≈13 。

  • 在特征图上需要将候选区域映射的区域划分为 k*k 个单元格，比如常见的 7*7，如上所述的候选区域特征图大小为 13*13，长宽划分为7等份，则需要再次取整来确定每个单元格的边界。

这样做存在不匹配问题（misalignment），特别实在特征图较小，原图中目标也较小的情况下，在特征图上少量偏差，比如0.8，假设特征图为原图的1/32，则在原图中偏差为32*0.8，这对于一些小目标检测，偏差十分明显。

ROI Align 的主要思想和具体方法

ROI Align的思路很简单：取消量化操作，使用双线性内插的方法获得坐标为浮点数的像素点在图像上的数值,从而将整个特征聚集过程转化为一个连续的操作。其操作流程如下：

  • 遍历每一个候选区域，保持浮点数边界不做量化。

  • 将候选区域分割成 k*k 个单元，每个单元的边界也不做量化。

  • 在每个单元中计算固定四个坐标位置，用双线性内插的方法计算出这四个位置的值，然后进行最大池化操作。

前面两步和ROI Pooling类似，只是取消了量化取整的过程。经过前面两步，可以得到k*k 个单元，在每个小单元中，取固定位置的四个点，这四个点的坐标必然是浮点数。我们可以将这四个点都看作是原图缩小32倍后的目标像素点，对于每个目标像素点，都可以用双线性插值的方法求得其像素值，然后对四个像素值进行最大值池化即可。